Condensateurs : Capacité, Energie EMMAGASINEE

Exercice 1

Déterminer la capacité équivalente des assemblages de condensateurs suivants si chacun a une capacité de $10 µF$ :

 
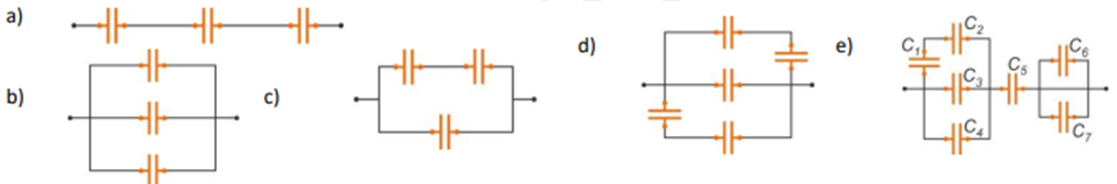
Exercice 2

Déterminer la capacité du condensateur équivalent $C_{AB}$ représenté ci-dessous :

 
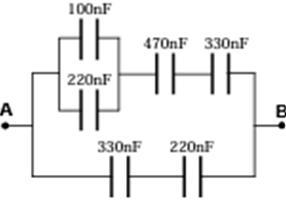
Exercice 3

Deux condensateurs, $C_{1} = 500 nF$ et $C_{2} = 750 nF$, sont branchés en parallèle à une pile de $12V$.
 
Une fois chargés, on débranche les condensateurs pour les brancher directement l’un à l’autre par leurs bornes de polarités contraires.

Après une nouvelle variation des charges déterminer : $q_{1}$ er $q_{2}$

Exercice 4

Dans le circuit ci-contre : $C_{1} = 10 µF, C_{2} = 20 µF, C_{3} = 30 µF, C_{4} = 40 µF,
C_{5} = 50 µF$ et $E = 15V$.

Déterminer :

1. La capacité équivalente;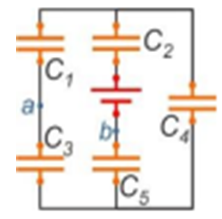

2. La charge du condensateur $C_{3}$;

3. La $d.d.p$. du condensateur $C_{5}$;

4. $V_{A} – V_{B}$.
     
Exercice 5

Le montage représenté ci-dessous représente la charge d'un condensateur $C = 10µF$ à l'aide d'une tension
$E = 5V$ constante et à travers une résistance $R = 2,2kΩ$.

L'interrupteur K est ouvert à partir de l'instant $t = 0$

 
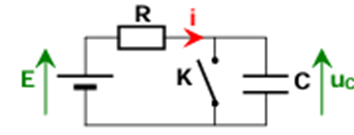
1. Quelle est la valeur de la tension $u_{C}$ avant l'ouverture de l'interrupteur $K$.
   
2. Par quel dipôle ($K$ ou $C$ ?) passe le courant $i$ avant l'ouverture de l'interrupteur $K$.
   
3. Calculer la valeur du temps $t_{1}$ au bout duquel la tension $u_{C}$ atteint $≈ 3,15V$.   

4. On réalise un autre essai avec $R$ réglable et on désire que la tension $u_{C}$ atteigne la valeur $4,75V$ au bout d'un temps $t_{2} = 10µs$.

Calculer alors la valeur de la résistance $R$

Exercice 6

Déterminer la tension de claquage $U_{max}$ puis la capacité $C$ d'un condensateur plan ayant des armatures de surface $S = 1cm^{2}$ distantes de $e = 0,01mm$ lorsque le diélectrique est successivement constitué d'air, de micas ou de mylar (tableau ci-dessous)
$$\begin{array}{|c|c|c|c|} \hline &\text{Air }&      \text{ Micas }&    \text{Mylar }\\ \hline \text{Champ disruptif }  E_{max} (V/m)&     3,2.10^{6}&     40.10^{6}&     200.10^{6}\\ \hline \text{Permittivité relative }  ε_{r}&     1&    6&    3\\ \hline \end{array}$$

    
Exercice 7

On charge un condensateur de capacité $C = 20 μF$, initialement non chargé, avec un générateur de courant d’intensité $I = 1,8 μA$.

1. Déterminer la charge $q$ acquise par le condensateur lorsque le circuit reste fermé pendant $10$ secondes.

2. Déterminer :

2.1. La tension $u_{AB}$ aux bornes du condensateur à l’instant $t = 10 s$.

2.2. L’énergie emmagasinée par le condensateur au bout de $t = 10s$
 

Exercice 8

1. On charge un condensateur par un courant constant $I_{0} = 0,30mA$ pendant $8s$.
 
La tension $U$ aux bornes du condensateur est alors de $12V$.
 
Quelle est la capacité $C$ du condensateur en $µF$?

2. Le  condensateur d’un flash électronique de capacité $150 µF$ est chargé avec une tension $U$  de $500V$.

Quelle est la valeur de la charge q portée par son armature positive ?

3. Quelle est l’énergie $E$ stockée par ce condensateur ?
 
Exercice 9

Un condensateur plan a les caractéristiques suivantes : $S = 350 cm²$ et $e = 4mm$.
 
Il est chargé sous une tension $U = 25 V$.
 
1. Calculer la capacité de ce condensateur dans le cas où le diélectrique est l'air.

2. Que devient-elle si on remplace l'air par du mica ?

3. Quel est l'intensité du champ électrique qui règne alors entre ces armatures ?

4. Sachant que le champ disruptif pour le mica est de $150 MV/m$ qu'elle est la tension qui détruira le condensateur ?

5. La tension de service à ne pas dépasser correspond au deux tiers de la tension destructrice.

Quelle est sa valeur ?

On donne : air sec : $ε_{r}=1 ;   mica: ε_{r}=7$.
 
Exercice 10

Calculer la capacité totale de:

1. 3 condensateurs en série : $10 μF, 10μF$ et $22 μF$;

2. 4 condensateurs en parallèle : $10 pF, 10 pF, 33 pF$ et $33 pF$;

3. 2 condensateurs en parallèle ($100 pF$ et $220 pF$) placés en série avec un 3ème de $220 pF$.

Exercice 11
 
Un condensateur de $100 μF$ est chargé sous une tension de $30 V$.
 
1. Quelle est la quantité d'électricité emmagasinée?

2. Quelle est l'énergie électrique emmagasinée?

Exercice 12
 
Un condensateur de $47μF$ et un autre de $33μF$ supportent la même tension maximale soit $25 V$.

On les branche en série puis en parallèle. Calculer dans chaque cas:

1. La capacité équivalente.

2. La tension maximale que peut supporter le groupement.

3. L'énergie emmagasinée par le groupement lorsqu'il est chargé sous la tension maximale.

Exercice 13

Un condensateur plan est formé par deux feuilles en aluminium, de surface en regard $S = 1m^{2}$, séparées par un isolant de permittivité relative $ε_{r} = 8$ et d’épaisseur $e = 0,1mm$.

1.  Calculer la capacité $C$ du condensateur.

2. Le condensateur est chargé sous une tension de $50 V$, calculer l’énergie qui $y$ est emmagasinée

Exercice 14

1. Les caractéristiques d'un condensateur sont les suivantes : $C= 0,12mF$, épaisseur du diélectrique
$e = 0,2mm$ ; permittivité relative de l'isolant : $ε_{r}= 5$ ; tension de service :$ Us = 100 V ; ε_{r}= 8,84 10^{-12} F/m$.

Calculer:

1.1. La surface des armatures.

1.2. La charge du condensateur soumis à la tension de service.

1.3. L'énergie emmagasinée dans ces conditions.

2. Le condensateur étant chargé, on l'isole, puis on l'associe en parallèle à un condensateur de capacité
$C_{1=} 0,15 mF$ initialement déchargé.

Calculer :

2.1. La charge totale de l'ensemble formé par les deux condensateurs.

2.2. La tension commune aux deux condensateurs en régime permanent.

2.3. L'énergie emmagasinée par le montage.

Exercice 15

On prend un condensateur de capacité $C_{1} = 470µF$ et chargé avec la tension $U_{1} = 24V$.   

Calculer la valeur de l'énergie $W_{1}$ emmagasinée par $C_{1}$.  

On prend un deuxième condensateur de capacité $C_{2} = 1000µF$ déchargé $(U_{2} = 0V)$.   

Quelle est la valeur de l'énergie $W_{2}$ emmagasinée par $C_{2}$.  

On branche maintenant les deux condensateurs $C_{1}$ et $C_{2}$ en parallèle.   

Déterminer la valeur de la tension U aux bornes des deux condensateurs   

Calculer la valeur de l'énergie $W_{12}$ emmagasinée par l'ensemble $C_{1} // C_{2}$

Comparer  $W_{12}$  avec $W_{1} + W_{2}$ et donner une explication au résultat.

Exercice 16

1. On construit un condensateur plan avec des armatures de $0,510 cm²$, qu’on séparera par une feuille de mica dont la constante diélectrique est $κ = 8$.

1.1. Déterminer l’épaisseur de cette feuille si on trouve une capacité de $7,50 pF$.

1.2. Avec la même feuille, quelle surface des armatures donnerait plutôt une capacité de $500 µF$?

2. Deux condensateurs identiques branchés en parallèle ont une capacité équivalente de $30 pF$.

Si on insère dans l’un d’eux un matériau dont la constante diélectrique est $κ = 2,40$, déterminer la capacité équivalente modifiée

3. Soit trois condensateurs identiques. Pour le $1er$ et le $2e$ condensateur, on insère entre les plaques des matériaux diélectriques tels que $k_{1} < k_{2}$

On ne modifie pas le $3^{e}$ condensateur. Placez en ordre croissant les capacités $C_{1}, C_{2}$ et $C_{3}$ des trois condensateurs

Exercice 17

On considère le circuit suivant :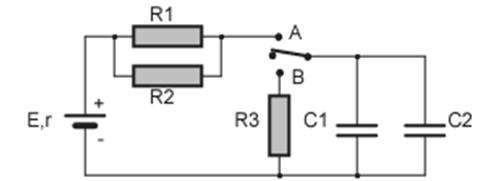
 
1. Commutateur sur la position A : on charge 2 condensateurs identiques, associés en parallèle, à travers un dipôle constitué de deux résistances égales en parallèle.

$E = 50 V$  ;  

$r\#0 Ω$  ;

$C_{1}= C_{2} = 0,1 µF$

1.1. Quelle est la valeur de la capacité équivalente ? $R_{1}, R_{2} = 200 kΩ$

1.2. Quelle est la valeur de la résistance équivalente ?

1.3. Quelle est la valeur de la pointe de courant à l'instant initial ?

1.4. Quelle est la constante de temps et la durée pratique de la charge des condensateurs ?

1.5. Quelle est l'énergie totale emmagasinée ?

1.6. Quelle est l'énergie emmagasinée par chaque condensateur ?

2. Commutateur sur la position $B$ : on décharge ces condensateurs dans la résistance $R_{3} = 100Ω$.

2.1. Quelle est la nouvelle valeur de la pointe de courant ?

2.2. Quelle la constante de temps de décharge.

2.3. Sous quelle forme et où l'énergie s'est-elle dissipée ?

Exercice 18

1. On branche un condensateur plan directement à une pile, et alors qu’il est toujours connecté, déterminer ce qu’il advient si on éloigne les armatures à :

1.1. La charge portée par les armatures;

1.2. L’intensité du champ entre les plaques;

1.3. La différence de potentiel entre les armatures;

2. On débranche ensuite le condensateur de la pile, et rapproche à nouveau les armatures.

Qu’adviendra-t-il de :

2.1. La charge portée par les armatures;

2.2. La différence de potentiel entre les armatures;

2.3. Le champ entre les plaques;

2.4. La capacité.

Exercice 19

On considère les trois condensateurs de la figure ci-contre, de capacités $C_{1}, C_{2}$ et $C_{3}$  chargés sous une différence de potentiel $V_{A}-V_{B}=5V$.

On donne : $C_{1}=5µF, C_{2}=10µF$ et $C_{3}=15µF$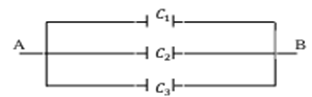     

1. Calculer les charges $Q_{1}, Q_{2}$ et $Q_{3}$ des condensateurs de capacités respectives $C_{1}, C_{2}$ et $C_{3}$  

2.1. Déterminer l’expression de la capacité équivalente $C$ entre les points $A$ et $B$

2.2. Calculer la valeur de la capacité équivalente $C$

3. En déduire l’expression de la charge   du condensateur équivalent.
4. Quelle est la relation entre $Q_{1}, Q_{2}, Q_{3}$et $Q$.

5. Calculer l’énergie électrostatique emmagasinée dans le condensateur équivalent

Exercice 20

On réalise le montage de la figure avec un générateur de courant, un interrupteur $K_{1}$, un ampèremètre et un condensateur montés tous en série, un voltmètre numérique et un interrupteur $K_{2}$ branchés aux bornes du condensateur.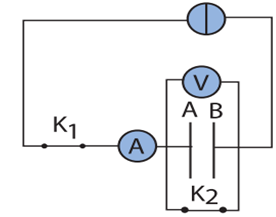

Avant toute mesure, on ferme l’interrupteur $K_{2}$, puis on l’ouvre et on le maintient ainsi durant toute l’expérience.

Simultanément, on ferme $K_{1}$ et on déclenche le chronomètre

Avec un chronomètre, on mesure toutes les $5$ secondes la tension $u_{c} = u_{AB}$      
Pour $I = 0,144 mA$ par exemple, on obtient les résultats consignés dans le tableau suivant :
$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline t (s)&     0&     5&     10&     15&     20&     25&     30\\ \hline
u c(V)&     0&     1,5& 3&     4,6&     6,1&     7,6&    9,2\\ \hline \end{array}$$

1. Que se passe-t-il quand on ferme $K_{2}$ ?

Quelle est l’indication du voltmètre ?

2. Avant de fermer $K_{2}$, le voltmètre peut indiquer une tension non nulle. Expliquer cette possibilité.

3. A l’aide du tableau des mesures dressé, montrer que la charge $q$ augmente avec $u_{c}$.

4. Tracer la courbe d’évolution de la tension $u_{c}$ aux bornes du condensateur en fonction de la durée de charge,

5. Montrer graphiquement que $u_{c} = kt$ où $k$ est une constante que l’on

calculera.

6. Déterminer la relation entre la charge $q$ du condensateur et la tension $u_{c}$ à ses bornes.

7. Déterminer le coefficient de proportionnalité $C$ et préciser son unité

Exercice 21

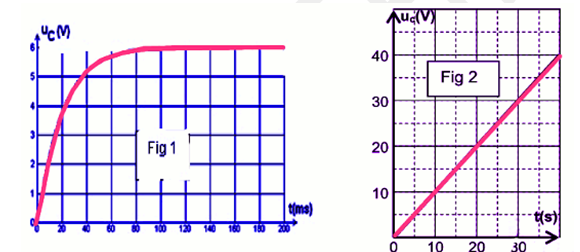
Le montage représenté ci-dessous permet de charger et de décharger un condensateur de capacité $C$ dans une résistance $R$.

 
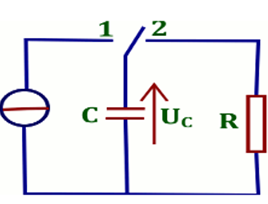
1.1. Pour chacune de ces deux opérations, quelle doit être la position de l’interrupteur?

1.2. Des deux graphes (fig1 et fig2) proposés ci-dessous, lequel qui correspond à la
charge du condensateur? Justifier

 
Le générateur de courant permet une charge, à intensité constante, d’un condensateur. La charge dure 40s et l’intensité du courant a pour valeur $1μA$.

2.1. Calculer la charge du condensateur à la date $40s$.

2.2. Quelle est la valeur de l’énergie emmagasinée par le condensateur à cette date ?

2.3. Calculer la capacité du condensateur.

3. Sachant que ce condensateur est plan et que l’aire des deux surfaces communes en regard est $S=0,1m^{2}$ et que l’épaisseur du diélectrique qui se trouve entre les deux plaques est $e=0,02mm$.

3.1. Déterminer la permittivité électrique absolue $ε$ du diélectrique de ce condensateur.

3.2. Déduire la permittivité relative $ε_{r}$ du diélectrique.
On donne $ε_{0}=8,85.10^{−12}F.m$