EXERCICE 1

  Un générateur de force électromotrice  $E = 6,0 V$ et de résistance interne $r = 10Ω$, est connecté, en série, à un rhéostat de résistance maximale égale à 90 $Ω$  et à une résistance de protection $R_{p}  = 220 Ω 1$.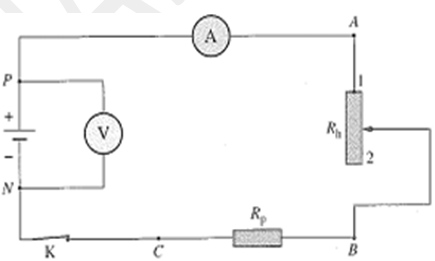
 
On veut mesurer la tension $U_{PN}$  et l’intensité $I$ du courant électrique.

indiquer, sur le schéma, la position de la borne  $COM$ sur les deux multimètres.

2. Déterminer les valeurs limites de l’intensité I du courant électrique dans le circuit, lorsque  le rhéostat est  en :      

2.1. Position $1$

2.2. Position $2$

3. On suppose désormais que l’intensité I du courant  est égale à $20 mA$

3.1. Donner l’expression des tensions aux bornes des différents  dipôles $U_{PN}, U_{Rh}$  et $U_{BC}$ puis les calculer

3.2. Déterminer la puissance électrique  reçue par le dipôle $BC$  

3.3. En déduire l’énergie électrique reçue par le dipôle $BC$, pour une durée $∆t= 5 min$ de fonctionnement.

Que devient cette énergie ?

3.4. Exprimer, puis calculer la puissance électrique cédée par le générateur au circuit

3.5. Exprimer, puis calculer la puissance électrique totale mise en jeu par le générateur

3.6. Expliquer  et justifier la différence entre les puissances calculées aux questions $b$ et $d$ ?

3.7. Déterminer la puissance électrique reçue par le rhéostat lors de ce fonctionnement.

En déduire la valeur de la résistance $R_{h}$ du rhéostat    entre la position $1$  et celle du curseur.

EXERCICE 2

On associe en série:  

- une batterie d'accumulateurs de $f.é.m. E = 24V $et de résistance interner $r=1,2 Ω$ ;

- un conducteur ohmique de résistance $R = 4,8 Ω$ ;  

- un moteur de $f.é.m. E$' et de résistance interne $r'$ ;  

- un ampèremètre de résistance négligeable.  
La $f.é.m. E'$ du moteur est proportionnelle à sa vitesse de rotation; sa résistance interne $r'$ est constante.  

1. On empêche le moteur de tourner: sa $f.é.m. E'$ est nulle, le moteur est alors équivalent à une résistance $r'$.

Le courant dans le circuit a une intensité $I_{1} = 2,1 A$.
 
1. 1 Faire un schéma du montage.

1. 2 Ecrire la relation entre $E, r, R, r'$ et $I_{1}$.  

1. 3 Exprimer r' en fonction de $E, r, R, r$ et $I_{1}$.  
1. 4 Calculer $r'$.
 
2. Le moteur tourne à la vitesse de $250 trs.min^{-1}$ en fournissant une puissance utile $P_{u} = 8,6W$.
 
L'intensité du courant est alors $I_{2} = 1,2A$.  

2.1. Exprimer $E'$ en fonction de $E, r, R, r'$ et $I_{2}$.  

2.2. Calculer $E'$  

2.3. Calculer la puissance consommée par chaque récepteur lorsque le moteur tourne.  

2.4. Faire un bilan énergétique de ce circuit.  

2.5. Calculer le rendement global de ce circuit.

EXERCICE 3

Un circuit série comprend :
-un générateur de $f.é.m. E =24V$ et de résistance interne $r= 0.5Ω$

- un résistor de résistance $R=8Ω$

-un ampèremètre de résistance négligeable

- un moteur de $f.c.é.m. E’$ et de résistance interne $r’ =1.5Ω$

-un voltmètre monté aux bornes du moteur

1. Représenter le schéma du circuit.

2. On empêche le moteur de tourner, préciser les valeurs de l’intensité du courant et de la tension indiquées respectivement par l’ampèremètre et le
voltmètre.

3. Le moteur tourne, l’ampèremètre indique une intensité $I_{1}= 1.8A$, déterminer

3.1. La valeur de l’intensité indiquée par le
voltmètre,

3.2. La $f.c.é.m. E’$ du moteur

3.3. Le rendement du moteur
4. Calculer les énergies mises en jeu dans chaque élément du circuit pendant $Δt=10min$.

EXERCICE 4

Un électrolyseur dont les électrodes sont en fer contient une solution aqueuse d'hydroxyde de sodium.

On le soumet à une tension continue réglable $U$ ; I est l'intensité du courant qui le traverse.

1.  Faire un schéma du montage en mettant en place les éléments suivants :

- générateur continu à tension de sortie réglable ;

- interrupteur.

- Rhéostat, électrolyseur, ampèremètre, voltmètre.

2. Les résultats des différentes mesures sont consignés dans le tableau suivant :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
U(V)&0&0.5&    1.0&    1.5&    1.6&    1.6&    1.8&    2&2.5&3&    3.5&    4&    4.5&  5\\
\hline
I(V)    &0&0&0&0&0.002&0.03&    0.05&0.1&0.29&0.5&0.71&0.92&    1.10    &1.32\\
\hline
\end{array}$$

2.1. Tracer la caractéristique intensité-tension de l'électrolyseur en prenant :

Echelles : en abscisses : 1cm pour $100 mA$; en ordonnées: $1 cm$ pour $0,5 V$.

2.2. Donner l'équation de la partie linéaire de cette caractéristique sous la forme : $U = a + bI$.

2.3. En déduire les valeurs, en unités $S.I$., de la $f.c.é.m. E'$ et de la résistance $r'$ de l'électrolyseur lorsqu'il fonctionne dans le partie linéaire de sa caractéristique.

2.4. L'électrolyseur précédent est désormais branché aux bornes d'une pile de $f.é.m. E=4,5V$ et de résistance interne $r= 1,50Ω $:

- Calculer l'intensité I du courant qui le traverse.

- Quelle puissance électrique Pe Reçoit-il ?

-  Quelle puissance PJ dissipe-t-il par effet joule ?

- De quelle puissance utile Pu dispose-t-il pour effectuer les réactions chimiques aux électrodes ?

2.5. Ecrire les équations bilan des réactions aux électrodes sachant qu'on observe :

- à l'anode : une oxydation des ions OH- avec dégagement de dioxygène ;

- à la cathode : une réduction de l'eau avec production de dihydrogène.

EXERCICE 5

1. Une dynamo qui fonctionne en générateur (loi d’Ohm reste valable) débite dans un circuit de résistance variable. La résistance interne $r = 0,5 Ω$.

On a relevé la tension $U$ aux bornes de ce générateur lorsqu’il débite un courant d’intensité $I$.

1.1. Compléter le tableau et en déduire la puissance engendrée pour $U = 76 V$.
$$\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline
I(A)&    0&    4&    8&    12&    16&    20&    24&    28\\
\hline
U(V)    &110&    107&    102&    97&91&84&76&    68\\
\hline
E(V)&&&&&&&&\\
\hline
\end{array}$$
                                
1.2. Représenter sur le même graphique les courbes $U = f (I)$ et $E = g (I)$ :
Echelle : $1cm \rightarrow  2A ; 1cm \rightarrow  5 V$

La dynamo tourne à $1800 tr.min^{-1}$ et débite un courant d’intensité $I = 22 A$.

1.3. Calculer le moment du couple qu’il faut appliquer sur le rotor de la dynamo.

Quel est alors le rendement électrique de cette dernière?  

2. La dynamo en série avec une résistance chauffante $R=7\omega$ débite un courant $I = 13A$

2.1. Quelle est, sous ce régime, la $f.é.m. E$ de la dynamo ?
 
2.2. La résistance $R$ plonge pendant une minute dans un calorimètre de capacité calorifique $µ=100J.K^{-1}$
contenant $200g$ d’eau.

Quelle est l’élévation de température du calorimètre ?

2.3. On intercale en série un moteur de $f.c.é.m. E’$ et de résistance interne $r’ = 1\ome$.

La dynamo de $f.é.m$.

$E=106 V$ débite un courant d’intensité $I = 8A$.
 
Donner le bilan énergétique du circuit. En déduire $E’$ et le rendement du circuit.

EXERCICE 6

Un générateur $G$, un rhéostat et un ampèremètre sont disposés en série.

Un voltmètre est branché aux bornes du générateur.

1. Pour différentes valeurs de la résistance du rhéostat, on relève les valeurs suivantes.
$$\begin{array}{|c|c|c|c|c|c|}
\hline
I(A)    &0&    0,1&    0,2&    0,4&    0,6&\\
\hline
U(V)    &12&    11,5&11&    10&9\\
\hline
\end{array}$$

1.1. Représenter le schéma du montage.

1.2. Pourquoi utilise-t-on le rhéostat dans le montage?

Expliquer le principe de fonctionnement.

1.3. Tracer la courbe $U= f(I)$ à l’échelle : $0,1A \rightarrow 1cm ; 2V \rightarrow 1cm$

1.4. Déterminer de la caractéristique la force électromotrice $E$ et la résistance interne $r$ de $G$.

1.5. Enoncer la loi d’ohm relative à un générateur.

2. On branche aux bornes du générateur un résistor de résistance $R$.

L’ampèremètre indique un courant
  d’intensité $I=0,6A$.
 
2.1. Calculer la tension aux bornes du générateur.

2.2. Comparer la tension aux bornes du générateur à celle aux bornes du résistor.

2.3. Calculer la résistance $R$ du résistor.

3. On relie les bornes du générateur par un fil conducteur de résistance très faible (supposée nulle)

3.1. Qu’appelle-t-on l’intensité du courant débité par le générateur dans ce cas ?

3.2. Calculer l’intensité de ce courant.

EXERCICE 7

Un circuit électrique est constitué d’un générateur G de $f.é.m. E$ et de résistance interne $r$.

Expérience 1 :

On branche aux bornes du générateur un résistor de résistance $R_{1} = 4Ω$.

Un ampèremètre placé en série dans le circuit indique $I_{1} = 2A$.

Expérience 2 :

On branche aux bornes du générateur un résistor de résistance $R_{2} = 1Ω$.

L’ampèremètre indique $I_{2}=4A$.
 

1. Ecrire la loi d’Ohm aux bornes de chaque dipôle.

 2. Déterminer les grandeurs caractéristiques $(E ; r)$ du générateur.

3. Le générateur G précédent de $f.é.m. E$ et de résistance interne $r$ est placé dans un circuit formé par un ampèremètre en série avec un rhéostat de résistance variable.
 
Une étude expérimentale a permis de tracer la caractéristique intensité-tension du générateur. (Figure ci-dessous) :
 
3.1. Représenter le schéma du circuit en indiquant les branchements de l’ampèremètre et du voltmètre

3.2. A partir du graphe, retrouver les valeurs des grandeurs caractéristiques du générateur.

3.3. Déterminer graphiquement et par le calcul la valeur de l’intensité du courant électrique de court-circuit $Icc$

3.4. On branche en parallèle avec le générateur G un électrolyseur $( E’= 8V ; r’=2 Ω)$.

3.5. En appliquant la loi de Pouillet, déterminer l’intensité du courant électrique.
 
3.7. Déduire les coordonnées théoriques du point de fonctionnement. Conclure quant à l’adaptation des deux dipôles.

EXERCICE 8

Une personne adulte consomme approximativement $170 L$ de dioxygène $O_{2}$ chaque jour, les spationautes utilisent des réserves $d’O_{2}$ en bouteille, mais pour des raisons de transport et de logistique, une partie de celui-ci est fourni par électrolyse.
 
Un électrolyseur permet de transformer de l’énergie électrique en énergie chimique et en énergie thermique (par effet Joule). En laboratoire, $2$ élèves ont réalisé le montage ci-dessous :

Voici un tableau récapitulant les mesures lors du fonctionnement de l’électrolyseur pour différentes tensions fournies par le générateur :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline
I(A)&0&    0&    0&    0&    0,020&    0,047&    0,061    &0,073&    0,100\\
\hline
U(V)&    0&    1,00&    2,00&    2,50&    3,00&    3,24&    3,39&    3,49&    3,73\\
\hline
\end{array}$$

1. A partir de quelle tension appliquée par le générateur, l’électrolyseur laisse-t-il passer le courant pour produire du dioxygène ?

Justifier votre
réponse.

2. Tracer la courbe $U = f(I)$ caractéristique de cet électrolyseur

3. Déterminer les valeurs de $E’$ et de $r’$ en précisant les unités de ces grandeurs.

4. En déduire l’expression numérique de la tension $U$

5. Compléter le diagramme de puissances de ce convertisseur.

Déterminer le rendement $η$ de cet électrolyseur et démontrer que $η= \dfrac{E’}{U}$.

Calculer le rendement $η$, en $%$, de cet électrolyseur pour une intensité de $50 mA$.
 
Un électrolyseur de ce type produit approximativement $23 mL$ de dioxygène par heure.

Dans la réalité, l’ISS est ravitaillé par des bouteilles de $O_{2}$.

Justifier que l’alimentation par des électrolyseurs du type étudié par les élèves n’est pas envisageable.

EXERCICE 9   Caractéristique d’une pile électrochimique

Au cours d’une séance de travaux pratiques, Axelle et Marius ont relié une pile électrochimique à un conducteur ohmique de résistance réglable.

Ils ont relevé la tension $U$ aux bornes de la pile en fonction de l’intensité $I$ du courant qu’elle délivre.

Ils ont obtenu les résultats des mesures dans le tableau ci-dessous.
$\begin{array}{|c|c|c|c|c|c|c|c|}
\hline
I (mA)&    0&    100&    200&    300&    400&    500&    600\\
\hline
U(V)&    4,70&    4,50&    4,40&    4,27&    4,13&    3,98&    3,82\\
\hline
\end{array}$$

1. Pour effectuer les mesures de tension et d’intensité, quels sont les appareils utilisés ?

2. Faire le schéma du montage électrique permettant d’effectuer les mesures.

Les appareils de mesure doivent apparaître. Indiquer le sens conventionnel du courant.

3. Tracer la caractéristique tension – courant $U = f(I)$ de cette pile sur le papier millimétré

4. Déterminer le coefficient directeur et de l’ordonnée à l’origine de la droite qui passe au plus près des points.

5. En déduire les valeurs de la tension à vide $E$ de la pile et de sa résistance interne $r$.

6. Déterminer la charge électrique $Q$ délivrée par la pile pendant $∆t = 5,0min$ si la tension à ses bornes est $U = 4,0V$.

Détailler vos calculs.

EXERCICE 10

On branche un générateur de $f.é.m. E$ et de résistance interne $r$ avec un électrolyseur de $f.c.é.m. E’$ et de résistance interne $r’$ (voir figure ci-dessous).

La durée de fonctionnement est $20min$.

1. Montrer que l’intensité du courant qui circule dans le circuit est $I=0.36A$ et la tension aux bornes de l’électrolyseur est $U=5.6V$.
 
2. Calculer :     

2.1. L’énergie fournie par le générateur.

2.2. L’énergie convertie en énergie chimique par l’électrolyseur.

2.3. L’énergie dissipée par effet Joule dans le circuit.

3. Calculer :

3.1. Le rendement de l’électrolyseur.

3.2. Le rendement du générateur.

3.3. Le rendement du circuit