EXERCICE 1

1. Soient deux points $A (2 ; 5 ; 7)$ et $B (0 ; 1 ; 2)$ d’un repère $(O, x, y, z)$, l’unité de longueur étant le décimètre.

Ces points sont dans un champ électrique uniforme  $E$.  

où  est le vecteur unitaire de $(Oz)$.

On constate que $V_{A} – V_{B} = - 50 V$.

En déduire $E$.

2. Soit un champ uniforme  $E$.

tel que $E = 300 V/cm$.$(O,\vec{i},\vec{j},\vec{k})$  est la base d’un repère orthonormal.

L’unité de longueur est le centimètre.

2.1. Calculer la d.d.p  entre les points $A (3 ; 2 ;
1)$ et $B (5 ; 0 ; 8)$.

2.2. On superpose au champ précédent le champ  $=E_{1}$.  avec $E_{1} = 400 V/cm$.

Calculer la nouvelle d.d.p entre les points $A$ et $B$.

EXERCICE 2 

Soient deux points $M$ et $N$ d’abscisses respectives $x_{M} = 10 cm$ et $x_{N} = 4 cm$ dans un champ électrostatique uniforme de vecteur champ  parallèle et de même sens que  $i$ et d’intensité $E = 2000 V/m$

1. Calculer, en $eV$,  le travail de la force électrostatique qui s’exerce sur une charge $q = 1,5.10^{-6} C$ dans ce champ.

2. Déterminer la différence de potentiel $V_{M} – V_{N}$

EXERCICE 3

On dispose de deux armatures $A$ et $B$ distantes de $d = 5cm$.

On applique une tension $U_{AB} = 300V$ entre ces armatures.

1. Représenter la tension $U_{AB}$ et le vecteur champ électrostatique . Préciser les caractéristiques de .

2. On choisit l’origine des potentiels en $B$.

Un point $N$ est situé à $0,5 cm$ de l’armature négative et un point $M$ à $1,5 cm$ de l’armature positive.

Calculer les potentiels en $M$ et en $N$.

3. Un ion $Al^{3+}$ se déplace de $M$ vers $N$ sur une droite faisant un angle $\theta = 60°$ avec les armatures.

Exprimer le travail de la force électrostatique que subit cet ion en fonction de e (charge élémentaire) et $U_{MN}$.

Calculer sa valeur.

4. Placer en pointillés et en vraie grandeur les équipotentiels $100V ; 150V$ et $200 V. e = 1,6.10^{-19}C$

EXERCICE 4

Une boule électrisée supposée ponctuelle de masse $5 cg$ porte une charge $q<0$.

Elle est placée en un point $O$ situé entre les armatures horizontales $A$ et $B$ d’un condensateur plan (voir figure ci-contre)

1. Lorsqu’on applique entre les armatures distantes de $d = 4 cm$ une tension $U_{AB}$ telle que $= 4 kV$ la boule est en équilibre

1.1. Quel est le signe de $U_{AB}$.

Justifier

1.2. Déterminer les caractéristiques du champ  crée par les armatures.

1.3. Calculer la valeur de $q$ portée par la boule.

2. Décrire qualitativement ce que l’on observerait dans les cas suivants :
    $U_{AB} = 4,5 kV$.

2.2. $U_{AB} = 3,5 kV$

EXERCICE 5

Un champ électrostatique uniforme   de norme $E = 10 kV.m^{-1}$ règne entre deux plaques verticales $P_{1}$ et $P_{2}$ ; distantes d’une distance et portées respectivement aux potentiels électriques $V_{1}$ et $V_{2}$.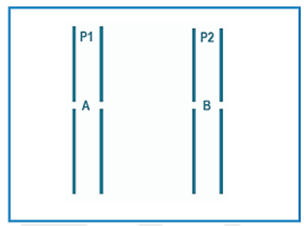

Un proton de charge
$q = +e$ et de masse m pénètre d’un trou $A$ de la plaque $P_{1}$ avec une vitesse supposée nulle ; il est accéléré vers un trou $B$ dans la plaque $P_{2}$.

On néglige l’effet du poids.

4.1. Représenter sur la figure le sens de $\vec{F_{e}}$ et de  $\vec{E}$
 
4. 2. Déduire le signe de $V_{2}-V_{1}$

4.3. Déterminer la valeur de la distance $d$.
 
4.4. Calculer en joule $(J)$ puis en $keV$, le travail de la force électrostatique de la plaque $P_{1}$ à la plaque $P_{2}$.
 
4.5. En appliquant le théorème de l’énergie cinétique exprimer la vitesse $v_{B}$ du proton au point $B$ en fonction de $e, E, d$ et $m$ puis calculer sa valeur en $km.h^{-1}$

4.6. Quelle doit être la valeur de d pour que la particule arrive à la plaque $B$ avec la vitesse qui vaut la moitié de la lumière dans le vide ?

On rappelle que la vitesse de la lumière dans le vide : $C=3.10^{8}ms^{-1}$

4.7. Calculer, en eV, la variation de l’énergie potentielle électrostatique entre $A$ et $B$
 
4.8. Sachant que $V_{1}= 0$ et $E_{pe_{A}}= 0$ calculer $E_{pe_{B}}$ par deux méthodes différentes.

On donne : $| V_{2}-V_{1}| = 500V ; e = 1,6.10^{-19}C$ et $m = 1,67.10^{-27}kg ; 1keV=1,6.10^{-16}J$   

EXERCICE 6

Un générateur maintient une tension $U = 200V$ entre deux plaques conductrices parallèles situées dans le vide.

1. Un électron quitte la plaque négative pour être capté par la plaque positive.

Calculer le travail de la force électrostatique qui s’exerce sur cet électron (en joules et en électronvolts).

2. La distance séparant les plaques est $d = 2cm$. Caractériser le champ électrostatique en tout point de l’espace compris entre les plaques.

3. On écarte les plaques, toujours parallèles, à $d’ = 4cm $; la tension de $200V$ est maintenue.

Reprendre les questions précédentes.

Conclure.

4. Les plaques sont déplacées de façon quelconque et ne sont plus parallèles.

 Peut-on toujours calculer simplement le travail de la force électrostatique qui s’exerce sur l’électron allant de la plaque positive à la plaque négative ?

EXERCICE 7

On maintient une $d.d.p$ de $1 000V$ entre deux plaques conductrices identiques, parallèles, distantes de $5cm$.

Une charge $q = 10^{-12}C$ se déplace entre les plaques d’un point $A$, situé à $1cm$ de la plaque positive, à un point $B$, situé à $2cm$ de la plaque négative.

1. Calculer le champ électrostatique entre les deux plaques.

2. Calculer la $d.d.p V_{B}-V_{A}= U_{BA}$.
 
3. Calculer l’énergie potentielle de la charge $q$ en $A$, puis en $B$, en prenant comme référence la plaque négative.

4. Calculer le travail de la force électrostatique s’exerçant sur la charge $q$ pour aller de $A$ en $B$

EXERCICE 8

Au voisinage de la Terre, près du sol, il existe un champ électrostatique uniforme, vertical et dirigé vers le sol.

Sa norme varie linéairement avec l’altitude selon la loi $E = a + bh$ entre les altitudes $h = 0$ et $h =1 400m$.

1. Sachant que pour $h = 0, E = 100V.m^{-1}$ et que pour $h = 1 400m, E = 20V.m^{-1}$, déterminer les constantes $a$ et $b$.

quelles sont leurs unités ?
Représenter graphiquement $E$ en fonction de $h$.

2. Par une méthode graphique, déterminer le travail des forces électriques s’exerçant sur une charge de $10^{-10}C$ se déplaçant de l’altitude $O$ à l’altitude $h$.

En déduire le potentiel électrostatique d’un point situé à l’altitude $h$ si l’on prend comme référence la surface terrestre.

3. Un ion $H^{+}$ est formé à l’altitude $h = 1 400m$.

Le champ de pesanteur est supposé uniforme, d’intensité
$g = 10m.s^{-2}$.

Calculer l’énergie potentielle de pesanteur et l’énergie potentielle électrostatique de cet ion.

Les comparer.

Si l’ion part de l’altitude $h = 1 400m$ avec une vitesse nulle, quelle sera sa vitesse à l’arrivée sur le sol (on négligera toutes les autres interactions) ?

EXERCICE 9

La sphère, supposée petite et chargée positivement, d’un pendule électrostatique est en équilibre en un point $O$ situé entre deux plaques $P$ et $N$ conductrices, parallèles et distantes de $d = 15cm$.

Les plaques sont initialement neutres. On applique une tension $U_{PN}= 1 500V$ entre les deux plaques.

La sphère chargée adopte, après quelques oscillations, une nouvelle position d’é d’équilibre $A$.

1. Calculer la charge $q$ du pendule si, à l’équilibre, l’angle $α$ que fait le fil de suspension avec la verticale vaut $30°$ ; la sphère est attirée du côté de la plaque négative $N$.

2. Le point $O$ est pris comme point de référence α est l’angle que fait le fil du pendule avec la verticale lorsque la sphère est attirée par la plaque $N$.

Pour $α⋲ [0 , \dfrac{π}{2} [$ , exprimer en fonction de $α$ l’énergie potentielle de pesanteur $E_{pg}$ et l’énergie potentielle électrostatique $E_{pe}$.

Représenter graphiquement $E_{pg}$ et $E_{pe}$ en fonction de $α$.

En déduire la représentation graphique de la somme $E_{P}$ de ces énergies potentielles.

Pour quelle valeur de $α$ cette somme est-elle minimale ?

Conclure.

Données : masse de la sphère :$ m = 0,5g$ ; longueur du fil : $l =20m ; g = 10 m.s^{-2}$

EXERCICE 10

Une particule $\alpha$ (noyau d'hélium), produite par une source radioactive, est émise au voisinage d'un point $A$.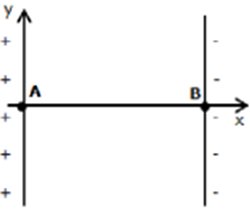
 
La valeur de sa vitesse en $A$ est négligeable devant celle qu'elle peut atteindre en $B$.

Entre les points $A$ et $B$ règne un champ électrostatique uniforme qui permet l'accélération de la particule.

Le poids et les frottements sont négligeables lors de ce mouvement.

1. Quelle est la charge $q\alpha$ de la particule $\alpha$ ?
 
2. Établir l'expression du travail de la force électrostatique s'appliquant sur la particule $\alpha$ se déplaçant entre $A$ et $B$.
      
Exprimer ce travail en fonction $q\alpha , V_{A}$ et $V_{B}$.

($V_{A}$ et $V_{B}$ sont les potentiels respectifs aux points $A$ et $B$.)

3. En déduire l'expression de la variation d'énergie potentielle électrique entre $A$ et $B$.
 
4. L'énergie mécanique se conserve-elle?

Justifier.

5. À partir des réponses précédentes, exprimer la différence de potentiel $V_{A} - V_{B}$ en fonction de $v_{B}, m\alpha$ et $q\alpha$ et calculer cette valeur sachant que la vitesse en $B$ a pour valeur $v_{B} = 1,00. 10^{3} km.s^{-1}$

Données : $e = 1,60 .10^{-19} C; m\alpha= 6,70.10^{-27} kg$.

EXERCICE 11

Les électrons pénètrent en $O$ entre les plaques $P_{1}$ et $P_{2}$ à la vitesse horizontale $v_{0}$ et ressortent en $M$.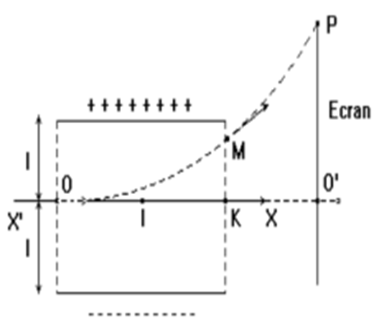

Le point $O$ est à la même distance $l=3cm$ des deux plaques et $v_{0} = 10^{7} m/s$.

1. On établit entre les plaques la tension $U_{P1P2} = U = 600 V$.

Déterminer la direction, le sens et l’intensité du champ électrostatique $E$, supposé uniforme, qui règne entre les plaques.

2. Déterminer les caractéristiques de la force électrostatique qui agit sur l’électron puis :

- la comparer à son poids et conclure ;

- justifier le sens de la déviation observée.
     
3. L’axe $X’OX$ pénètre dans le champ électrique en $O$ et en ressort en $K$

- Montrer que la $d.d.p$ entre les points $O$ et $K$ est nulle.

- Calculer la $d.d.p$  sachant que $MK = 1,3cm$.

En déduire la valeur de la $d.d.p$

4. Calculer la vitesse $v$ acquise par ce dernier à sa sortie du champ au point $M$.

5. La trajectoire de l’électron entre $O$ et $M$ est un arc de parabole et on montre (nous l’admettons) que la tangente en $M$ à la parabole passe milieu de $OK$.

- A partir de $M$, en dehors de tout champ, quelle sera la trajectoire de l’électron ?

- L’électron rencontre l’écran fluorescent $(E)$, au point $P$.

Calculer le déplacement vertical ou déflexion électrique $O’P$.

 Données : longueur des plaques $ℓ=10cm ; IO’ =40cm$

EXERCICE 12

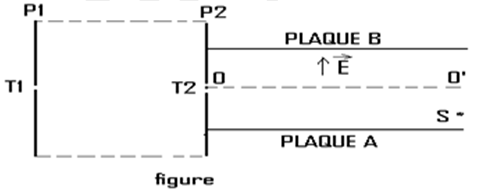
Entre les plaques verticales $P_{1}$ et $P_{2}$ distantes de $d = 16 cm$ est appliquée une différence de potentiel de valeur absolue $|V_{P_{1}}-V_{P_{2}} |=80V$

1. Un électron animé d’une vitesse $V_{1} = 5.106 m.s^{-1}$ est émis du trou $T_{1}$ de la plaque $P_{1}$ et se dirige en ligne droite vers la plaque $P_{2}$ (voir figure).

1.1. Déterminer le signe de la différence de potentiel  V_{P1}-V_{P2} entre les plaques $P_{1}$ et $P_{2}$.

1.2. Déterminer les caractéristiques du vecteur champ électrostatique $\vec{E^{{0}}$ entre les plaques $P_{1}$ et $P_{2}$ et le représenter.

1.3. Calculer le travail de la force électrostatique $\vec{F}$ pour faire passer l’électron de la plaque $P_{1}$ à la plaque $P_{2}$.

En déduire la vitesse $V_{2}$ avec laquelle l’électron arrive au trou $T_{2}$.

1.4. Calculer en joule puis en keV l’énergie cinétique de la particule à son arrivée au trou $T_{2}$.

2. A la sortie du trou $T_{2}$ l’électron pénètre avec la vitesse $T_{2}$ entre les plaques $A$ et $B$ horizontales ou règne un champ électrostatique uniforme $\vec{E}$ représenté dans la figure.

L’électron entre par le point $O$ situé à égale distance des deux plaques.

La distance entre les deux plaques $A$ et $B$ est $d = 8 cm$.

Lorsque la tension
$U_{AB} = 500 V$, l’électron sort de l’espace champ en un point S tel que $O’S = 1,5 cm$.

2.1. On prend l’origine des potentiels $V_{0} = 0$ du point $O$, calculer $V_{S}$  potentiel électrostatique du point $S$.

2.2. Déterminer $Ep(O)$ et $Ep(S)$ énergies potentielles électrostatiques de l’électron en $O$ et en $S$.
Données : $e = 1,6.10^{-19} C ; m_{e} = 9,1.10^{-31} kg ; 1eV = 1,6.10^{-19} J$

EXERCICE 13

Deux plaques parallèles métalliques $P$ et $N$ verticales et distantes de $d = 10cm$ sont soumises à une tension positive $U = V_{P} – V_{N} = 10^{2}V$.

Entre ces deux plaques existe, un champ électrostatique $\vec{E}$ .

Soient deux points $A$ et $B$ distants de $d’$, d’une ligne de champ où $A$ est le point le plus proche de la plaque $P$.

On fera une figure soignée.
1.1. Donner la direction et le sens de vecteur $\vec{E}$.

Justifier.

1.2. Exprimer la norme de $\vec{E}$ en fonction de $U$ et $d$. Calculer sa valeur.

1.3. Quel est le signe de la tension $U_{AB}$.

Justifier.

1.4. Exprimer la tension $U_{AB}$ en fonction de $U, d$ et $d’$.

2. Un électron est placé au point B dans le champ $\vec{E}$.

Dans tout ce qui suit, on considéra que le poids de l’électron est négligeable devant la force électrostatique.

2.1. L’électron est-il susceptible d’atteindre le point $A$.
Justifier.

2.2. Exprimer le travail de la force électrostatique $\vec{F}$ appliquée à l’électron entre $B$ et $A$ en fonction de $e, U, d$ et $d’$.

2.3. Sachant que l’électron part du point $B$ sans vitesse initiale et arrive en $A$ avec une vitesse $v =4,2.10^{6}m/s$, déterminer l’expression du travail de cette force entre $B$ et $A$ en fonction de $m, v$.

2.4. En déduire l’expression de la distance $d’$ entre $A$ et $B$ en fonction de $m, e, U, v$ et $d$.

Données : $e = 1.6.10^{-19}C ; m = 9,1.10^{-31}kg$

EXERCICE 14

On considère le schéma ci-contre.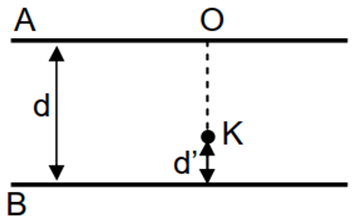

Les plaques $A$ et $B$ sont distantes de $d = 10cm$.

La plaque $A$ est négative. Des ions $Fe^{2+}$ et $Cl^{-}$ arrivent au point $O$ avec la même vitesse $v = 50km/s$.

La tension entre les plaques $A$ et $B$ est telle que $U_{AB} = U = - 10^{3}V$.

1.1. Représenter $\vec{{E}$ (le champ entre les plaques $A$ et $B$), puis la force électrostatique $\vec{{F}$ appliquée à chaque type d’ions dans le champ$\vec{{E}$.
      
1.2. En déduire les ions susceptibles de traverser le champ$\vec{{E}$. .

Justifier.
 
2. On veut que l’autre type d’ions puisse traverser le champ$\vec{{E}$.  .

Que doit-on faire ?

3. Les plaques restent disposées comme l’indique la figure ?

Les ions $Fe2^{+}$ rebroussent chemin à partir d’un point $K$ situé à une distance d’ de la plaque $B$. (Voir schéma)

3.1. Etablir l’expression du travail de la force électrostatique appliquée à l’ion $Fe^{2+}$ en fonction de $U, e, d$ et $d’$.

3.2. Donner l’expression de la variation de l’énergie cinétique entre $O$ et $K$ en fonction de $U, e, d$ et $d’$.

3.3. En déduire l’expression de $d’$en fonction de $m, v, e, U et d ; m$ étant la masse de l’ion $Fe^{2+}$ et $v$ sa vitesse en $O$.

Calculer la valeur de $d’$.

4.1. Exprimer la variation de l’énergie potentielle des ions Fe2+ entre $A$ et $K$ en fonction de $e, U, d$ et $d’$.

4.2. En prenant le point $A$ comme état de référence, donner l’expression du potentiel $V_{K}$ au point $K$ en fonction de U, d et $d’$.

Calculer sa valeur.
Données : $m (Cl^{-}) = 5,8510-26kg ; m (Fe^{2+}) = 9,32.10^{-26}kg$.

Le poids des ions est négligeable

EXERCICE15

Un pendule simple, constitué d’un fil inélastique $OC$ de longueur $l = 50cm$, de masse négligeable, fixé par son extrémité $O$ et d’une petite bille en cuivre assimilable à un point matériel de masse $m = 1g$, fixé en $C$.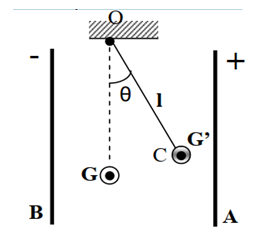
 
Le pendule est placé entre deux plaques métalliques $A$ et $B$ planes, verticales parallèles, séparées d’une distance  $d = 20cm$.

La bille porte une charge électrique $q$ et les plaques sont soumises à une tension $U_{AB} = 25kV$.

Le pendule s’écarte d’un angle $θ =15°$. (Voir figure).    
 
1. Quelle est la nature du champ électrostatique créé entre les plaques ?

2. Représenter sur un schéma les forces extérieures appliquées à la bille.

3. Exprimer l’intensité de la force électrostatique appliquée à la bille en fonction de $m, g$ et $θ$

4. En déduire la valeur de la charge $q$.

5. Déterminer le travail effectué par la force électrostatique lorsque le pendule passe de la position initiale $G$ à sa position
d’équilibre $G’$.

6. En déduire la différence de potentiel entre $G $et $G’$

EXERCICE 16

On considère un pendule électrostatique simple constitué d'une bille conductrice, portant une charge $q$ positive, suspendue à
l'extrémité d'un fil isolant et inextensible.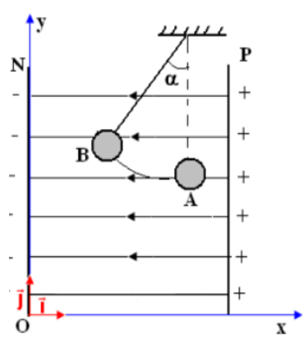

Le pendule est suspendu en point $O$ entre les plaques $P$ et $N$ (les armatures) d’un
condensateur.

Lorsqu’on applique une tension entre les plaques $P$ et $N$ :

- Les plaques acquièrent des charges électriques opposées

- Un champ électrique uniforme est alors crée entre deux plaques

-la bille se déplace vers l'armature $N$ en faisant un angle par rapport à la normale (la charge $q$ est transportée de point $A$$ (point de départ) vers point $B$ (point d’arrivée)     

1. Déterminer les caractéristiques (direction et sens) du vecteur champ électrique $\vec{E}$ crée entre deux plaques

2. Représenter les lignes de champ électrique à l’intérieur du condensateur

3. Ecrire la relation entre la force électrostatique $\vec{F}$ agissant sur la bille chargée et le vecteur champ électrique$\vec{E}$.

4. Monter que la force électrostatique est constante puis représenter la force sans souci d’échelle sur la figure lorsque la bille est en $A$ et en $B$

5. Établir l'expression du travail que fournit la force électrostatique $\vec{F}$ lors du déplacement de la bille chargée entre $A$ et$ B$

6. Le travail de la force électrique dépend-il du chemin suivi par la bille chargée entre ses positions initiale (point $A$) et finale (point $B$) ?

EXERCICE 17

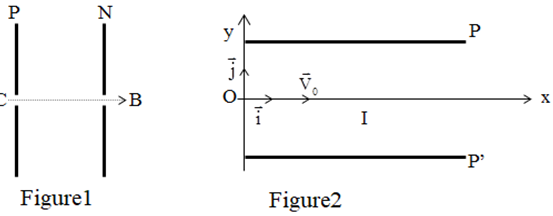
Entre deux plaques $P$ et $N$ verticales on applique une tension $U_{PN}$ de valeur absolue $U$ (figure 1)

1. Un électron pénètre en $C$ avec une vitesse quasi nulle et ressort en $B$ avec une vitesse $V_{B}$.

Quel doit être le signe de $U_{PN}$ ?

Calculer $V_{B}$.

On donne : $U = 500 V ; m_{e} = 9,1.10^{-28} g$.

2. Des noyaux d’hélium $(_2^3)He^(2+)$ et $(_2^A)He^(2+)$  de masses respectives $m_{1} = 3.u$ et $m_{2} = A$.$u (u$ est l’unité de masse atomique $1 u = 1,67.10-27 kg$) pénètrent en $C$ avec une vitesse négligeable devant leur vitesse de sortie respectives $V_{1}$ et $V_{2}$ en $B$.

2.1. Quel est le signe de $U_{PN}$ ?

2.2. Ces noyaux ont-ils la même énergie cinétique ? Justifier.

2.3. Etablir la relation entre $V_{1},V_{2}$ et $A$.

Calculer $A$ pour $V_{1} =7,99.105 m/s$ et  $V_{2}=6,92.105m/s$

3. Entre deux plaques $P$ et $P’$ distantes de $d = 2,5 cm$ et de longueur $l = 10 cm$ règne une $d.d.p U=U_{PP’}$ de valeur absolue $400V$.

Un faisceau de proton homocinétique arrivent et $O$ avec une vitesse $V_{0} = 800 km/s $et sort du champ $\vec{E}$ au point S avec une vitesse $\vec{V_{S}}$ (figure 2).

L’équation de la trajectoire des protons est donnée dans le repère $(O, \vec{i}, \vec{j})$ par $y=\dfrac{qEx^{2}}{2mv_{0}^{2}} ( q$ est la charge du proton et $m_{p}$ la masse du proton).

On appelle déviation du faisceau l’angle $\alpha= (SI ; IH)=(V_{0} ; V_{S})$ où $I$ est le milieu du segment $[OH]$

3.1. Exprimer $\alpha$ en fonction de $e$ (charge élémentaire), $U, l, d, m_{p}$ et $V_{0}$.

Calculer $\alpha$.

3.2. En déduire la vitesse $V_{S}$ de sortie des protons.

3.3. Déterminer la $d.d.p USH$
 
3.4. Calculer numériquement la valeur de $U$ à ne pas dépasser si l’on veut que le faisceau sort du champ électrique sans être capté par la plaque $P$.

EXERCICE18

Deux armatures métalliques $P_{A}$ et $P_{B}$, parallèles entre elles et distantes de $d$, sont reliées aux bornes d'un générateur de tension continue.

Entre ces deux armatures règne un champ électrostatique $\vec{E}$ uniforme.

1. Donner l'expression du travail de la force électrostatique $(\vec{E})$ qui s'exerce sur une particule de charge $q$ se déplaçant d'un point $A$ de l'armature $P_{A}$ à un point $B$ de l'armature $P_{B}$.
 
L'exprimer en fonction de $E, AB$ et $q$.

2. Montrer que le travail de cette force s'écrit : $W_{AB} (\vec{F}) = q.U_{AB}$.

3. Calculer sa valeur dans le cas d'un noyau d'hélium $He^{2+}$ se déplaçant de $A$ à $B$.

Données : $e = 1,60.10^{-19} C; U_{AB}= 400 V$.