EXERCICE 1

On considère le circuit schématisé (figure 1) et le graphe (figure 2) ci-dessous

 
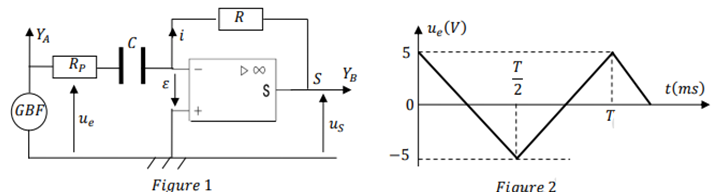
1. Préciser le type de montage de la  figure1.

Justifier la réponse.

2. Dire le rôle de la résistance $R_{P}$ montée en série avec le condensateur $C$ pour un montage pratique.

3. Le $GBF$ délivre un signal triangulaire (voir  figure2).

Ce signal est injecté à l’entrée du circuit.

3.1. Représenter sur le même graphe, les signaux obtenus sur les sorties $Y_{A}$ et  $Y_{B}$ de l’oscillographe comme indiqué sur la figure1.

3.2. Donne la forme du signal $uS$ à la sortie du circuit.

On donne : $R= 1000ῼ; C = 0,2µF$ et fréquence du $GBF: f= 1000Hz$

EXERCICE 2

Un montage intégrateur est construit en utilisant un $A.O$ parfait, un condensateur de capacité $C = 0,5 µF$ et un conducteur ohmique de résistance$ R = 20 k Ω$.

1. Faire le schéma du montage.

On mettra en évidence la borne d’entrée $E$ du montage, la borne de sortie $S$ et la masse $M$.

2. On applique entre $E$ et$ M$, une tension $U_{e} = V_{E} - V_{M}$ dont les variations au cours du temps sont représentées par la courbe ci-dessous.

2.1. Déterminer la période $T$ et la fréquence $N$ de $U_{e}$.

2.2. Montrer que la tension d’entrée $U_{e}$ est proportionnelle à tout instant, à la dérivée de la tension de sortie $U_{s} = V_{S} - V_{M}$ .

Conclure.

3. Calculer de façon littérale, puis numérique, la valeur du coefficient de proportionnalité

 EXERCICE 3

Après le cours sur montages dérivateur et intégrateur, un élève en classe de $Tle C$ se rend à la bibliothèque de son établissement pour $y$ faire des recherches dans le but de consolider ses acquis.

Une fois à la bibliothèque, il découvre dans un document cet exercice.

Tu es sollicité(e) pour l’aider à répondre aux questionnaires

 
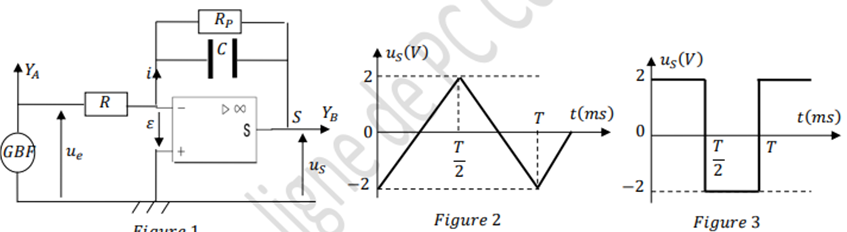
On donne $R = 10KΩ; C = 0, 2µF$ et la période $T = 2ms$.

1. Préciser si le circuit est intégrateur ou dérivateur.

Justifie ta réponse.

2. Dire le rôle de la résistance $R_{p}$ montée en parallèle avec le condensateur $C$ pour un montage pratique.

3. On visualise le signal $uS$ à la sortie du circuit sur la voie $C$ d’un oscillographe bicourbe
(figure 2).

3.1. Représenter le signal $u_{e}$ à l’entrée du circuit.

3.2. Donner la forme du signal d’entrée $u_{e}$

4. On change le signal à l’entrée du circuit.

Le signal $uS$ à la sortie du circuit est représenté sur la figure 3.

Préciser la nature du signal délivré par le $GBF$.

EXERCICE 4

On considère le circuit schématisé ci-dessous.

 
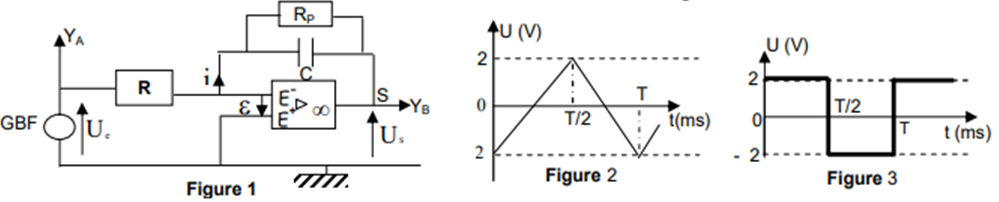
On donne $R=10 kῼ , C = 0,2µF$ et la période $T= 2ms$.

1. Le circuit est-il intégrateur ou dérivateur ?

Justifier la réponse.

2. Quel est le rôle de la résistance $R_{P}$ montée en série a

3. On visualise le signal à la sortie $(U_{S})$ du circuit sur la voie $B$ d’un oscillographe bicourbe (Figure 2).

3.1. Représenter le signal $(U_{e})$ à l’entrée du circuit.

3.2. Quelle est la forme du signal à l’entrée $U_{e}$ ?

4. On change le signal à l’entrée du circuit.

Le signal à la sortie du circuit $(U_{S})$ est représenté sur la figure

3. Quelle est la nature du signal délivré par le $GBF$ ?

EXERCICE 5

On réalise le montage schématisé sur la figure 1. $L’A.O$ est parfait et fonctionne en régime linéaire.
$V_{sat} = ^{+}_{-}13V$.

On donne $R = 104 Ω$ et $C = 20µF$.

La tension d’entrée est représentée sur la figure $2$.

 
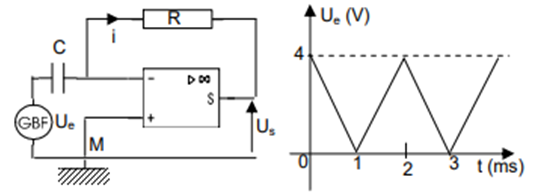
2. Calculer la fréquence $N$ de la tension d’entrée $U_{e}$.

3. Pour $0< t < 1ms$, établir l’expression littérale de $U_{e} = f(t)$ en fonction de $U_{max}$ et de la période $T$, donc de la fréquence $N$.
 
En déduire l’expression littérale de Us de $R, C, U_{max}$ et $N$.

Pour que le fonctionnement de $l’A.O$ reste linéaire, la fréquence $N$ doit être inférieure à une valeur $N_{0}$.

Exprimer $N_{0}$ en fonction de$ V_{sat}, R, C$ et $U_{max}$.

Calculer $N_{0}$

4. Reproduire le graphique $U_{e} = f(t)$ et le compléter en représentant la tension de sortie $U_{s}$

 EXERCICE 6

La tension $u_{1}$ est appliquée à l’entrée d’un montage avec un amplificateur opérationnel idéal.

A la sortie du montage, on observe la tension $u_{2}$.

 
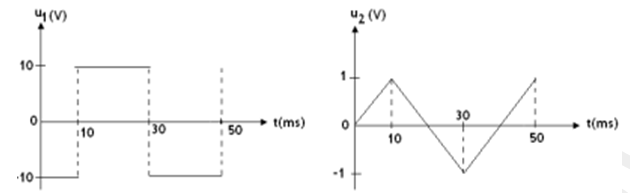
1. De quel montage s’agit-il ?

Faire le schéma de ce montage.

2. Etablir la relation liant $u_{1}$ et $u_{2}$.

3. Le résistor utilisé dans ce montage a une résistance $R = 1kΩ$.

Calculer la capacité du condensateur du circuit.

EXERCICE 7

1.1 Quel type de signal obtient-on à la sortie d’un montage dérivateur lorsqu’on applique à l’entrée un signal continu ?

Un signal en dent de scie ?

1.2. Quel type de signal obtient-on à la sortie d’un montage intégrateur si le signal à l’entrée est en créneaux ?

2.1. Dans un montage dérivateur, on utilise $C = 0,25μF$ et $R = 10 kΩ$.

La tension à l’entrée est un signal triangulaire alternatif de fréquence $N = 500Hz$ et d’amplitude $U = 1V$.
 
Représenter sur un même graphique et sur deux périodes, ce signal et celui observé à la sortie du montage.

2.2. On branche à la sortie du montage un résistor de résistance $R_{S} = 10 kΩ$.

Représenter sur le même intervalle de temps l’intensité du courant dans le résistor.

EXERCICE 8

Soit le montage suivant :

 
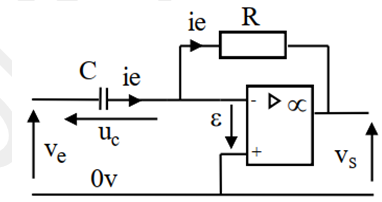
1. Quelles sont les hypothèses utilisables pour l’étude de ce montage ?

2. Rappels sur le condensateur :

On rappelle que pour le courant : avec $q$ quantité d’électricité qui traverse le conducteur.

L’intensité du courant représente donc la quantité d’électricité par unité de temps.

On rappelle que pour le condensateur : $q i_{e}= C\dfrac{du_C}{dt}$, avec $q$ charge portée par une armature, $C$ capacité du condensateur et $u_{c}$ tension aux bornes du condensateur.

Donner l’expression de $i_{e}$ en fonction de $C$ et $u_{c}$.

3. Donner la relation entre $V_{e}$ et $u_{c}$.

4. Donner l’expression de $i_{e}$ en fonction de $V_{s}$ et $R$

5. Donner l’expression de $Vs$ en fonction de $V_{e}, R$ et $C$.

6. Soit l’oscillogramme de la tension d’entrée $V_{e}$, Calculer pour$ 0≤t≤\dfrac{T}{2}$la variation $\dfrac{\Delta V_{e}}{\Delta t$

7. Application numérique.

Pour le dérivateur étudié, on donne : $R=10kῼ$ et $C=100nF$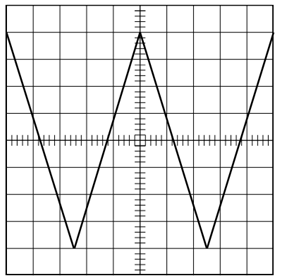

Calculer le produit $RC$.

8. Donner la valeur de la tension de sortie $V_{s}$ pour $0 \geq t \geq T/2$.

9. Calcul de variation.

Calculer pour $T/2  \geq t \geq 0$ la variation $\Delta V_{e}/\Delta t$.

10. Tension de sortie pour $T/2 \geq t \geq 0$.

Recommencer le calcul et donner la valeur de la tension de sortie $V_{s}$ pour $T/2 \geq t \geq T$.

11. Dessiner sur la même courbe la tension $V_{s}$.
 
Base de temps : $1ms / cm$ Sensibilité : $0,5v /cm$

 EXERCICE 9

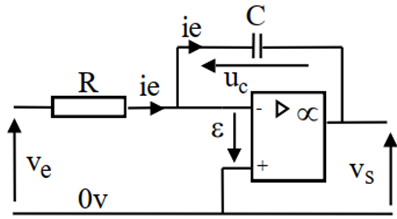
1. Quelles sont les hypothèses utilisables pour l’étude de ce montage ?

2. Donner l’expression de $i_{e}$ en fonction de $C$ et $u_{c}$.

3. Donner la relation entre  et $u_{c}$.

4. Donner l’expression de $i_{e}$ en fonction de $V_{e}$ et $R$

5. Donner l’expression de $i_{e}$ en fonction de $V_{s}$ et $C$.

6. Donner l’expression de $V_{e}$ en fonction de $v_{s}, R$ et $C$.

7. On donne l’oscillogramme de $V_{e}$ : .

Donner la valeur de la demi-période du signal d’entrée $T/2$ et la valeur de l’amplitude de la tension $V_{e}$.

8. On donne $R = 10 kΩ$ et $C = 10 nF$.

Donner la valeur du produit $RC$.

9. Donner la caractéristique et la valeur de $i_{e}$ pendant la première demi-période

10. Sachant que le courant est constant, quelle est l’allure de $uc(t)$.

On définit la variation de la tension aux bornes du condensateur : $\Delta uc = uc(t) – uc0$ qui correspond à la variation de temps
$\Delta t = t – 0 = t$.

On rappelle que $i_{e} = C duc/dt$ ce qui donne pour des variations finies $i_{e}  = C(\Delta uc /\Delta t)$.

Donner l’expression de $uc(t)$ en fonction de $I_{e} , t, C$ et $u_{c}0$.
 
11. Application numérique : On admet qu’en $t = 0 ms,u_{c}(0) = u_{c}0 = -10 V$.

Pour $0 < t < T/2$ donner

l’expression numérique de $u_{c}(t)$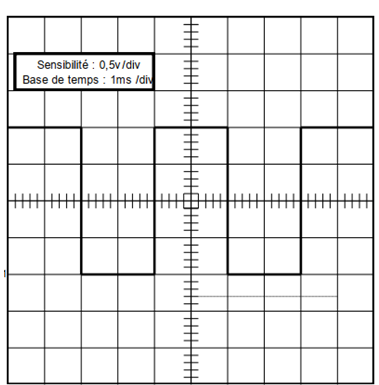

12. Donner la valeur de $u_{c}(T/2)$.

On rappelle que $T/2 = 2 ms$.

13. Pendant la $2ème$ période, donner les caractéristiques de $i_{e} $ .

Quelle est sa valeur ?

14. Expression de $u_{c}$ pour $T/2 \geq t \geq T$.

Sachant que le courant est constant, quelle est l’allure de $u_{c}(t)$ ?

15. Pour simplifier les calculs on fait un changement d’origine des temps.

On fixe l’origine des temps à $T/2$.

On note la nouvelle variable de temps $t’$.

Donc $t’ = t – T/2$.

Grâce à cette méthode on obtient comme précédemment avec la nouvelle variable :     
$U_{c}(t’)=\dfrac{I_{e}}{C}t’+u_{c}0$

Application numérique : On admet que en $t’ = 0 ms u_{c}(0) = u_{c}0 = +10V$.

Pour $0 < t’ < T/2$ donner l’expression numérique de $u_{c}(t’)$

Attention : pour alléger la notation, $u_{c}(t')$ sera noté simplement $u_{c}'$ dans l'expression.

16. On rappelle que en $t’ = T/2, t = T$.
 
Donner la valeur de $u_{c}$ en $t’ = T/2$.

On rappelle que $T/2 = 2ms$.

17. Signal de sortie :
On rappelle que $V_{s} = -u_{c}$ et que l'étude réalisée jusqu'ici porte sur $u_{c}$.

Donner l’expression de $V_{s}(t)$ en fonction de $R, C$ et $V_{e}(t)$ et tracer cette courbe