TRAVAIL ET PUISSANCE MECANIQUES
EXERCICE 1
Le point d’application d’une force F se déplace selon le trajet $ABCD$ repéré dans le plan à l’aide d’un repère orthonormé $(O,\vec{i},\vec{j})$.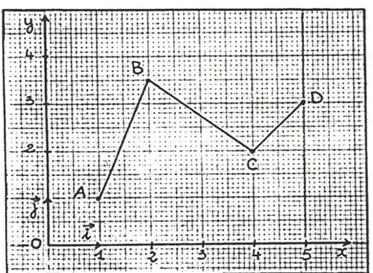
L’unité de longueur est le mètre.
Cette force est constante et a pour expression : $(\vec{F} )= 200\vec{i}, - 100\vec{i}$ en ($N$).
1. Calculer $W_{AB} (\vec{F}$, $W_{BC} (\vec{F} )$ et $W_{CD}( (\vec{F} )$ ainsi que la somme $W(\vec{F} )$ de ses travaux.
2. Calculer $W_{AD}(\vec{F} )$
3. Comparer $W( (\vec{F} )$ et $W_{AD}( (\vec{F} )$ Ce résultat est-il prévisible ? Justifier la réponse
EXERCICE 2
1. Une locomotive et son convoi constitue un seul système de masse $M=600$ tonnes.
La puissance de la force de traction, constante, a pour valeur $P = 24.105 W$ lorsque le train roule à la vitesse constante
$V = 144km/h$ sur une voie rectiligne et horizontale.
1.1. Calculer la force de frottement qui s’oppose à l’avancement du système.
1.2. Déterminer l’angle d’inclinaison de la réaction par rapport à la verticale.
2. Le système {locomotive-convoi} roulant toujours à vitesse constante gravit une voie dont la pente est de $3%$.
La puissance développée par la nouvelle force motrice est toujours de $24.105 W$ et la résultante des forces de frottement est $f = 6.104 N$.
2.1. Déterminer l’intensité de la nouvelle force motrice.
2.2. Déterminer la vitesse du système.
2.3. Quels sont : le travail de la nouvelle force motrice, le travail du poids et celui de la force de frottement pour un déplacement de $1km ?$
2.4. Calculer la somme des travaux de toutes les forces appliquées au système et conclure.
Donnée : $g=10N/Kg$
EXERCICE 3
Sur la ligne de plus grande pente d’une côte à $2%$ se déplace sans frottements à vitesse constante, une voiture de masse $100kg$.
La vitesse de la voiture reste constante sur une distance de $50m$.
1. Quelle est l’intensité de la force motrice ?
2. Calculer le travail de chacune des forces appliquées à la voiture au cours de ce déplacement.
3. Quelle est la puissance de la force motrice lorsque la voiture se déplace à la vitesse de $20km.h^{-1}$ ?
EXERCICE 4
Une charge de masse $m = 50kg$ est élevée d’une hauteur $h$ de deux façons différentes.
On la soulève d’abord verticalement, puis on la tire sur un plan incliné d’angle $α = 30°$ par le rapport à l’horizontale.
Dans les deux cas, le mouvement est rectiligne uniforme.
Sur le plan incliné la corde de traction reste parallèle au plan incliné.
On donne $g = 10 N/kg$ et $h = 5m$.
1. Dans chaque cas, calculer le travail effectué par chaque force extérieur à la charge, conclure.
2. Quel est alors l’intérêt du plan incliné?
EXERCICE 5
Un skieur de masse $m = 75kg$ (avec tout le matériel) descend une piste inclinée d’un angle $α = 14◦$ avec l’horizontale à une vitesse constante de $20m.s^{-1}$.
Les forces de frottements de la piste sur les skis ainsi que celle de l’air ont une résultante $(\vec{f} )$ ⃗parallèle à la pente.
1. Faire l’inventaire des forces agissant sur le skieur.
2. Calculer la valeur des forces de frottements.
3. Quel est le travail de cette force lorsque le skieur parcourt une distance de $250m$ dans ces conditions ?
4. Quel est le travail du poids du skieur pour ce même parcours ?
En déduire la puissance du poids.
5. Que vaut, dans ce cas, la somme des travaux de toutes les forces s’exerçant sur le skieur ?
EXERCICE 6
Une skieuse est tirée à vitesse constante, par un remonte-pente, sur une piste verglacée rectiligne de longueur $L =300 m$, faisant un angle $α=20°$ avec l’horizontale.
La tige du remonte-pente fait un angle $β=30°$ avec la direction de la piste.
La masse de la skieuse équipée est $m = 58 kg$.
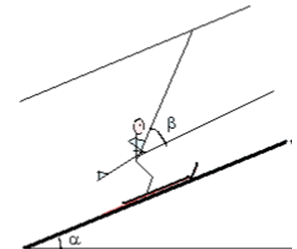
1. Faire un bilan des forces s’exerçant sur la skieuse et les représenter sur un schéma.
La force exercée par la tige est parallèle à sa direction et les frottements sont négligeables.
2. Quelle relation existe-t-il entre les forces appliquées à la skieuse ?
3. Quel est le travail de la résultante des forces ?
4. Exprimer le travail de chaque force.
5. En déduire la valeur de la force de traction exercée par la tige.
Donnée : $g = 9,8 N / kg$
EXERCICE 7
Une automobile de masse $m = 1200kg$ gravit une côte de pente constante $8%$ à la vitesse de $90km/h $
Le moteur développe une puissance constante $P = 30kW$.
L’air et les frottements divers qui s’opposent à la progression du véhicule équivalent à une force unique $(\vec{f} )$, parallèle au vecteur vitesse, de sens opposé et d’intensité $f = 260N$
1. Quel est, pour une montée de durée $1min$
a. Le travail $W_{m}$ effectué par le moteur (c’est à dire le travail de la force motrice développée par le moteur et qui provoque le mouvement du véhicule) ;
b. Le travail $W((\vec{P} ))$ développé par le poids du véhicule
c. Le travail $W((\vec{f} ))$ de la force $(\vec{f} )$
Quelle remarque ces résultats numériques vous suggèrent- il ?
2. Quelles sont les puissances $P((\vec{P} ))$ et $P((\vec{f} ))$ du poids $(\vec{P} )$ et de la force $(\vec{f} )$.
Données :
-une route de pente $8%$ s’élève de $8m$ pour un parcours de $100m$ le long de la route ;
- intensité de la pesanteur $g = 9, 8N/kg $
EXERCICE 8
Un disque de masse $m =100g$, de rayon $r = 20 cm$ tourne autour de l’axe perpendiculaire au disque en son centre.
1. Il est animé d’un mouvement de rotation uniforme, entretenu grâce à un moteur qui fournit une puissance de $36 mW$.
Un point $A$, situé à la périphérie du disque est animé d’une vitesse de $2,4m/s$.
1.1. Calculer la vitesse angulaire du disque.
1.2. Calculer la vitesse du point B situé à $2cm$ du centre du disque.
1.3. Calculer le moment du couple moteur.
1.4. Calculer le travail effectué par le couple moteur quand le disque tourne de $10$ tours.
2. On coupe l’alimentation du moteur : le disque s’arrête au bout de $8 s$ après avoir tourné de $7,6$ tours.
Le frottement peut être représenté par une force constante, d’intensité $1,5.10^{-2} N$, tangente au disque.
.2.1 Calculer le travail de cette force pendant cette phase du mouvement.
2.2. Calculer la puissance moyenne de la force de frottement durant cette phase.
2.3. Calculer la puissance (instantanée) de la force de frottement au commencement de cette phase.
EXERCICE 9
On fait tourner un treuil de rayon R avec une vitesse angulaire constante $ω=104 tr.min^{-1}$ grâce à un moteur de puissance $P=1 ,00kW$.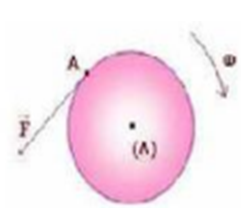
1. Trouver le moment Mm du couple moteur que l’on considère constant.
2. Déduire le travail effectué par le moteur pour que le treuil réalise dix tours.
3. A un moment on supprime le couple moteur et on applique une force de freinage $\vec{F}$ tangente au treuil comme l’indique la figure à coté, et il s’arrête après avoir freiné pendant cinquante tours complets.
Calculer le travail de cette force de frottement. On donne $F=25,00N R=0,50m$
EXERCICE 10
Un pendule simple est constitué d’une petite boule de rayon négligeable et de masse $m=100g$ suspendue à l’extrémité d’un fil indéformable de masse négligeable et de longueur $L=1m$ .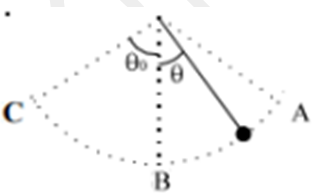
le pendule oscille entre deux positions $A$ et $B$ avec élongation maximale $0_{0}=40°$ comme le montre la figure.
1-calculer le travail du poids de la boule entre $A$ et $B$.
2. Calculer le travail du poids de la boule entre $B$ et $C$.
3. Déduire le travail du poids de la boule entre $A$ et $C$.
Justifier ce résultat
4. Calculer le travail de la force exercée par le fil.
EXERCICE11
On soulève un corps solide (S) de masse $m = 2kg$ à vitesse constante $v = 2m/s$ à l’aide du dispositif ci-contre et qui est constitué de :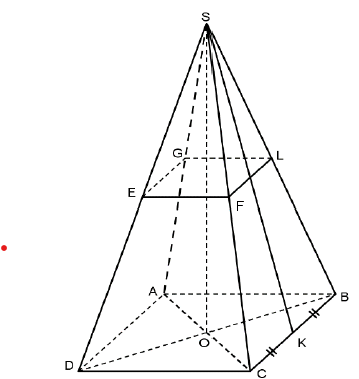
* Poulie à deux gorge de rayon $R = 10cm, r = 4cm$
* $f_{1}$ et $f_{2}$ deux fils enroulés chacun sur une gorge, les frottements étant négligeables
1. Calculer l’intensité de la force $\vec{F}$ appliquée sur le fil $f_{1}$
2. Calculer les travaux et les puissances des
deux forces $\vec{F}$ et $\vec{p}$. lorsque la poulie fait un tour complet
EXERCICE 12
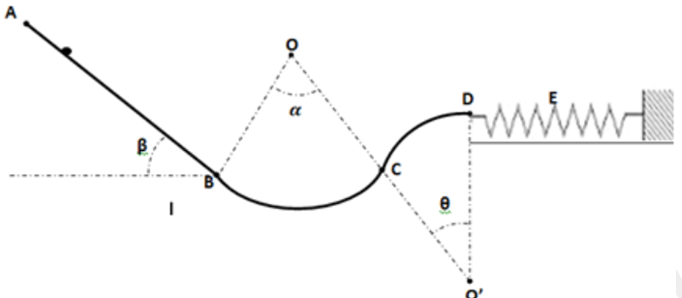
Un mobile de masse $m= 200 g$ considéré comme ponctuel se déplace le long d'une glissière lisse $ABCDE$ située dans un plan vertical.
La piste $ABCDE$ comprend quatre parties :
-une partie $AB$ rectiligne de longueur $L= 2m$ inclinée d'angle $\beta= 30°$ par rapport à l’horizontale.
-une partie circulaire $BC ̂ $de rayon $r_{1} = 50 cm$ tel que $BOC ̂ = \alpha= 60°$ ;
-une partie circulaire $CD$ de rayon $r_{2}= r_{1}$ tel que $CO’D= θ= 45°$ ;
-une partie rectiligne $DE$.
Tout au long de la piste, les frottements sont équivalente à une force unique $\vec{f}$ d'intensité $f = 0,5N$.
Sur la partie horizontale, on place un ressort de constante de raideur $K= 50N.m^{-1}$ dont l’extrémité libre coïncide avec le point $D$ de la piste.
Les points $B$ et $C$ sont sur la même horizontale.
3.1. Déterminer le travail de chacune des forces qui s'exercent sur le mobile pendant les trajets$ AB$ et $BC$.
3.2. Le mobile a parcouru la distance AB à la vitesse constante $V=1,5m/s$.
3.2.1. Evaluer la puissance développée par chacune de ces forces au cours du trajet $AB$.
3.2.2. Calculer la durée $∆t$ de parcours du mobile sur le tronçon $AB$.
2.3. Déterminer le travail de chaque des forces qui s'exercent sur le mobile pendant la montée $CD$.
4. Arrivé au point $D$, le mobile rencontre l’extrémité libre d’un ressort placé horizontalement.
Le ressort subit alors une compression $DE= x= 10cm$.
Calculer le travail effectué par la force élastique d’un ressort et celui du poids du mobile lors la compression de $D$ à $E$
EXERCICE 13
1. Une locomotive et son convoi constitue un seul système de masse $M=600tonnes$.
La puissance de la force de traction, constante, a pour valeur $P = 24.105 W$ lorsque le train roule à la vitesse constante $V = 144km/h$ sur une voie rectiligne et horizontale.
I.1.Calculer la force de frottement qui s’oppose à l’avancement du système.
I.2.Déterminer l’angle d’inclinaison de la réaction par rapport à la verticale.
II. Le système {locomotive-convoi} roulant toujours à vitesse constante gravit une voie dont la pente est de $3%$.
La puissance développée par la nouvelle force motrice est toujours de $24.105 W$ et la résultante des forces de frottement est $f = 6.104 N$.
II.1.Déterminer l’intensité de la nouvelle force motrice.
II.2.Déterminer la vitesse du système.
II.3.Quels sont : le travail de la nouvelle force motrice, le travail du poids et celui de la force de frottement pour un déplacement de $1km$ ?
II.4 Calculer la somme des travaux de toutes les forces appliquées au système et conclure.
Donnée : $g=10N/Kg$
EXERCICE 14
Un disque de masse $m =100g$, de rayon $r = 20 cm$ tourne autour de l’axe perpendiculaire au disque en son centre.
1. Il est animé d’un mouvement de rotation uniforme, entretenu grâce à un moteur qui fournit une puissance de $36 mW$.
Un point A, situé à la périphérie du disque est animé d’une vitesse de $2,4m/s$.
1.1. Calculer la vitesse angulaire du disque.
1.2. Calculer la vitesse du point $B$ situé à $2cm$ du centre du disque.
1.3. Calculer le moment du couple moteur.
1.4. Calculer le travail effectué par le couple moteur quand le disque tourne de $10 tours$.
2. On coupe l’alimentation du moteur : le disque s’arrête au bout de $8 s$ après avoir tourné de $7,6 tours$.
Le frottement peut être représenté par une force constante, d’intensité $1,5.10^{-2} N$, tangente au disque.
2.1. Calculer le travail de cette force pendant cette phase du mouvement.
2.2. Calculer la puissance moyenne de la force de frottement durant cette phase.
2.3. Calculer la puissance (instantanée) de la force de frottement au commencement de cette phase.
