EXERCICE 1

Un corps solide S de asse $m=5kg$ part sans vitesse initiale d’un point $A$ sous l’action d’une force motrice constante comme le montre la figure suivante et qui s’applique sur lui seulement entre $A$ et $B$.

Sachant que le corps arrive au point $E$ avec une vitesse nulle (la partie $DEF$ du trajet est un arc de cercle de rayon $r=1,5m$), on considère que les frottements sont négligeables (le long de le parcourt).

 
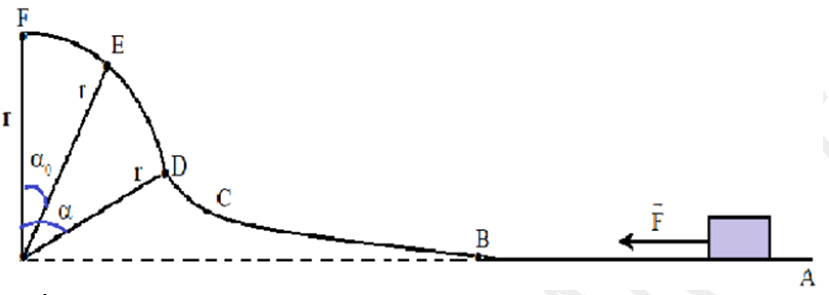
$α= 300 ; α_{0}= 1500 ; AB=r/2$

3.1. Donner l’énoncé du théorème de l’énergie cinétique

3.2. En appliquant le théorème de l’énergie cinétique sur le corps entre $B$ et $E$, déterminer sa vitesse lors de son passage par le point $B$ puis calculer sa valeur

3.3. En appliquant le théorème de l’énergie cinétique entre$ A$ et $B$, déterminer l’intensité de la force $F$ en fonction $m, g$ et $α_{0}$ ; puis la calculer

3.4. Sachant que pendant son retour du point $E$ le corps S se déplace vers le point $A$

En appliquant le théorème de l’énergie cinétique sur le corps $S$ entre $D$ et $E$, déterminer l’expression de la vitesse $v_{D}$ du corps lors de son passage par le point $D$ en fonction $m, g, α_{0}$ et $α$ ; puis calculer sa valeur

3.5. Quelle vitesse qu’il fallait donner au corps au point $B$ pour qu’il arrive au point $F$ avec une vitesse nulle ?

Et dans ce cas quelle sera l’intensité de la force $\vec{F}$ ?

EXERCICE 2

Afin de limiter le nombre d'accidents, nombreuses actions ont été mis en place.

La masse moyenne des véhicules neufs vendus est passé de $900kg$ en $1984$ à $1250 kg$ en $2008$.

1. Calculer l’énergie cinétique d’une voiture de $900 kg$ roulant à $90km/h$.

2. Calculer l’énergie cinétique d’une voiture de $1250 kg$ roulant à $90km/h$.

En $2002$, le conseil national de la sécurité routière français examinait un rapport d’experts qui ont étudié l’influence de masse du véhicule sur la gravité des accidents.

Ils ont montré que le taux d’usagers externes tués augmente avec la masse du véhicule.
3. D’après ce que vous avez vu en cours, pouvait-on prévoir cette influence de la masse d’un véhicule sur le taux de mortalité des usagers externes ? Justifier.

Pour faire bonne figure en matière de consommation de carburant, la voiture du futur devra être encore plus légère.

Toyota a récemment imaginée ce poids plume à travers le concept-car $1/X$, présenté au dernier Salon de Genève au mois de mars $2008$.

Grâce à l'utilisation massive de matériaux composites, le poids de cette auto hybride n'excède pas les $450$ kilogrammes.

4. Calculer l’énergie cinétique de la Toyota $1/X$ roulant à $90 km/h$.

5. Comparer cette valeur avec celle trouvée lors de la première question. Est-ce cohérent ? Justifier.

6. D’après vous, l’argument de légèreté de cette voiture est-il seulement lié à la
sécurité en cas de choc ?

EXERCICE 3

1. Un disque vertical, mobile autour de l'axe horizontal passant par son centre a un moment d'inertie $J=0,5kg.m^{2}$

Il est mis en mouvement par une force d'intensité constante $F = 20 N$ constamment tangente au disque dont le rayon est $R = 12 cm$.

Calculer la vitesse atteinte par le disque après avoir effectué une rotation de $20$ tours.

2. Un disque de masse $m = 200 g$, de rayon$ $R = 20 cm$, est animé d’un mouvement de rotation uniforme autour de son axe.

Sa vitesse angulaire est $ω = $120 tr/min$.

2.1. Quelle est la vitesse d’un point $M$ situé à $5 cm$ du centre du disque?

2.2. Quelle est le moment d’inertie du disque par rapport à son axe?

2.3. Pour entretenir ce mouvement, un moteur exerce un couple de moment $M$ dont la puissance est $P=500mW$.
Que vaut $M$ ? Montrer que des frottements interviennent et calculer le moment du couple de frottement agissant sur le disque.

2.4. A un instant donné, le moteur est débrayé et dès lors, on applique une force $F$ tangente au disque d'intensité $0,2 N$).

En supposant que le couple de frottement dont le moment a été calculé précédemment continue à agir, (en gardant toujours ce même moment), calculer le nombre de tours effectués par le disque avant qu’il ne s’arrête.

Donnée : $g = 9,8 N/Kg$

EXERCICE 4

On réalise le montage représenté ci-contre constituée de :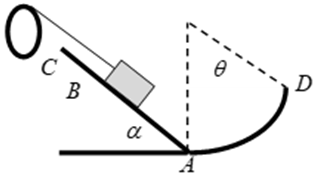

-poulie de rayon  qui peut tourner sans frottement autour de d’un axe fixe  passant par son centre symétrie sous l’influence d’un couple moteur de moment   

-un corps de masse $m=3kg$ attaché à l’extrémité d’un fil inextensible, de masse négligeable, glisse sans frottement sur un plan incliné d’un angle  $\alpha=30°$  avec le plan horizontale

- $AD$ rail circulaire de rayon $R=10cm $ et de centre   $0$
 
On donne  $AB=40cm ;j_{\Delta}$   

A l’instant  $T_{0}=0$, on libère le système sans vitesse initiale de la position    , le corps $(s)$ arrive à la position    avec   

En appliquant le théorème de l’énergie cinétique sur $(s)$ et sur la poulie.

montrer que  $T=\dfrac{m(rM_{m}+g\sin\alpha}{J_{\Delta}+mr^{2}}$
 
Sachant que $\vec{T}$  est l’influence du fil sur $(s)$ .

calculons $T$ et déduire la valeur de  $V_{B}$

1.2. Calculer la puissance en $B$  de $T$ ; de $\vec{P}$ (poids du corps $(s))$ et de   $M_{m}$

1.3. En  ; on fait bruler le fil et enlever le couple moteur en appliquant sur la poulie un couple résistant  ; la poulie fait $20$ tours avant d’être arrêtée.

Quelle distance va parcourir le corps $(s)$ avant son arrêt depuis le point  

1.4. Quelle est la valeur de    ?

2. En   le point de son arrêt ; en fait le corps

$(s)$ revient en décrivant la trajectoire   avec des frottements assimilables à une force tangente à la trajectoire ; opposée au sens du mouvement
 
2.1. Donner l’expression de   $W_{\vec{CD}} \vec{P}$  et $W_{\vec{CD}} \vec{P}   ; \vec{R}$  est la force de contact réparti exercée par  sur le corps(s)

2.2. Sachant que (s) s’arrête en  $D$; montrer que   ; en déduire sa valeur

EXERCICE 5

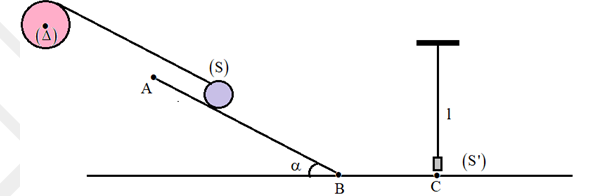
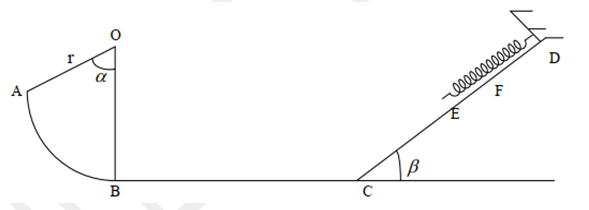
Un solide considéré comme ponctuel, de masse $m=400g$ pouvant glisser sur une piste formée de deux parties :

-une partie $AB$ de longueur $L=125cm$ inclinée d’un angle $α=30°$ par rapport à l’horizontale.

Les frottements sur la partie $AB$ sont négligeables.

-une partie horizontale $BC$ de longueur $d=80cm$. Les forces des frottements sont équivalentes à une force   opposée à la vitesse $v$ de $(S)$.

-une poulie homogène de rayon $r=4cm$ et d’axe$ (Δ)$, de moment d’inertie par rapport à cet axe,
$J_{Δ}=1,6.10^{-4} Kg.m^{2}$ ; les frottements dus à l’axe $(Δ)$ sont équivalents à un couple de moment constant $M_{c}=-8.10^{-3}N.m $

-Un fil inextensible et de masse négligeable assure la liaison entre la poulie et le corps $(S)$.

-Un pendule constitué d’un corps $(S’)$ ponctuel, suspendu à un fil inextensible   de masse négligeable, et de longueur $l=12cm$.
 
On prend $g=10N.kg^{-1}$
Lorsqu’on abandonne le système sans vitesse initiale, le corps $(S)$ se trouve en $A$, à l’instant $t_{A}=0$.

1. Exprimer le travail de la force exercée par le fil sur le corps $(S)$, entre les instants $t_{A}$ et $t_{B}$, en fonction de $m, v_{B}, g, L$ et $α$.

2. Exprimer le travail de la force $T′$ exercée par le fil sur la poulie, entre les instants $t_{A}$ et $t_{B}$, en fonction de $J_{Δ}, v_{B}, r, M_{c}$ et $L$

Montrer que :

$V_{B}=\sqrt{\dfrac{2L(mg\sin\alpha+\dfrac{M_{c}}{r})}{m+\dfrac{J_{\Delta}}{r^{2}}}}$ (sachant que $W( \vec{T}) = −W(\vec{T'} ))$.

Vérifier que $v_{B}=3m.s^{-1}$

A la date $t_{B}$, le corps $(S)$ arrive au point $B$, le fil se détache de la poulie, celle-ci continue à tourner et s’arrête après avoir effectué $n$ tours.

4. Déterminer le nombre $n$.
 
Le corps $(S)$ continue son mouvement sur la piste $BC$ et arrive au point $C$ par la vitesse $vC=2,8m.s^{-1}$

5. Déterminer l’intensité $f$ de la force de frottement.

Au point $C$, le corps $(S)$ heurte le corps $(S’)$ au repos, en lui communiquant $25.5%$ de son énergie cinétique. Sachant que$(S’)$  prend au point $C$ la vitesse $vc’=2m.s^{-1}$

6. Déterminer la masse m’ du corps $(S’)$ .
 
7. Déterminer l’angle $θ$ donnant la position d’arrêt du corps $(S’)$, en appliquant le théorème de l’énergie cinétique à $(S’)$ entre la position $C$ et la position d’arrêt (sachant que $W_{t} =0 $  car la force  $T$ du fil est tangente à la trajectoire circulaire de $(S’))$.

 

EXERCICE 6  

Un solide $(S)$ de masse $m = 1kg$ assimilable à un point matériel est lancé à partir d’un point $A$ sur un plan incliné d’un angle $\alpha= 30°$ par rapport à l’horizontale avec une vitesse $v_{A}=6 m/s$.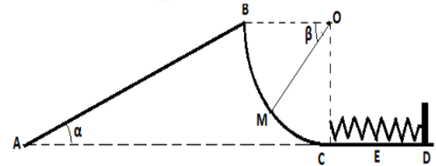

1. On suppose les frottements négligeables et le plan suffisamment lisse.

Calculer la longueur l que devrait parcourir $(S)$  avant de s’arrêter.
     
2. En réalité, on constate que $(S)$  parcourt une distance $AB = l_{1} = 3,2m$ le long du plan incliné.

En déduire l’intensité $f$ supposée constante des forces de frottement qui s’exercent sur $(S)$  entre $A$ et $B$.

3. Le mobile $(S)$  aborde maintenant, sans vitesse initiale, une piste formée de deux parties : une partie circulaire $BC$ de centre $O$ et de rayon $r = 1 m$ et une partie rectiligne $CD$.

On suppose qu’il existe des frottements équivalents à une force unique s’exerçant sur le solide sur toute la piste $BCD$ dont l’intensité
$f’ = 1,27 N$.

La position de l’objet sur la piste $BC$ est repérée par l’angle$ \beta = (OB, OM)$.

3.1. Exprimer la vitesse de $(S)$  au point $M$ en fonction de $r, f’, g, m$ et $β$.

3.2. Calculer cette vitesse au point $C$.

4. Arrivé en $C$ avec une vitesse de $4 m/s$, le solide aborde la partie $CD$ et l’extrémité libre du point $C$ d’un ressort de constante de raideur $k = 2500 N/m$ et le comprime d’une longueur $CE=x$.

Déterminer $x$.

EXERCICE 7

On considère une bille de masse m assimilable à un point matériel, suspendue à un fil inextensible de longueur $l$.

Le fil est fixé en un point $O$.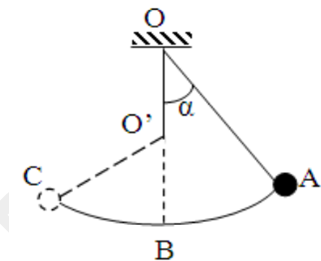

Tous les frottements sont négligeables.

1. Tout en gardant le fil tendu, on écarte la masse $m$ de sa position d’équilibre d’un angle $\alpha$ et on lâche sans vitesse initiale.

1.1. Représenter toutes les forces appliquées à la bille, lorsqu’elle est au point $A$.

1.2. Calculer la vitesse de la bille quand elle passe en $B$ situé sur la verticale passant par $O$.
     
2. Quand la bille passe en $B$, le fil bute conte une Tige fixée en $O’$.

La bille dans sa course monte jusqu’au point $C$ et redescend.

2.1. Représenter les forces appliquées à la bille au point $C$.

2.2. Calculer le travail de chacune des forces appliquées à la bille pour partir du point B au point $C$.
 
On donne : $m = 10 g ; l = 80 cm ; OO’ = 30 cm ; α = 60° ; g = 10 N.kg^{-1}$

EXERCICE 8

Un pendule est constitué d’une tige de longueur $AB =2L$ et de masse $M = 6m, m$ étant une masse de valeur donnée.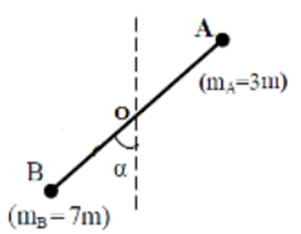

Cette tige est munie de deux masselottes quasi ponctuelles placées en $A$ et $B$ ; elles ont pour masse $m_{A} = 3m$ et $m_{B}= 7m$ (voir figure).

Le pendule composé oscille sans frottement dans un plan vertical.

1. Calculer le moment d’inertie $J$ du pendule pesant ainsi constitue.

2. On écarte le pendule d’un angle $\alpha = 50°$.

On le lâche sans vitesse initiale. Calculer la vitesse angulaire $ω_{0}$ lorsque celui-ci passe par sa position verticale.
     
3. Calculer alors la vitesse $V_{B}$ de la masselotte placée en $B$.

On donne : $m = 50 g ; L = 0,80 m$ et $g = 9,8 N/kg$

 EXERCICE 9   

Etude d’une petite bille

1. Mise en mouvement de la bille.

Un ressort de masse négligeable, à spires non jointives, a un coefficient de raideur $k=40N/m$ et une longueur à vide $l_{0}= 20cm$.

L’axe du ressort est horizontal.

Il est fixé à son extrémité droite par un support fixe.
 
A son extrémité gauche, une bille de masse $m =50g$ est placée contre une butée $P$.

Ce ressort va être utilisé pour lancer la bille dans une gouttière.

On comprime le ressort ; sa longueur devient $l=8cm$ ; on libère le système. La bille quitte la butée lorsque le ressort reprend sa longueur initiale.

 
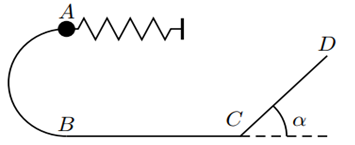
En supposant les frottements négligeables, établir l’expression littérale de la vitesse $v_{A}$ avec laquelle la bille quitte le ressort puis effectuer l’application numérique.

2. Mouvement de la bille dans la gouttière située dans un plan vertical.

La gouttière $ABCD$ sert de parcours à cette bille supposée ponctuelle. $g=9,8m · s^{-2}$.

Les frottements sont négligés, la gouttière étant parfaitement lisse. $AB$ est un demi-cercle de rayon $r=0,5m$ La bille part de $A$ avec la vitesse $v_{A}$ précédente.

2.1. Enumérer et représenter en $M$ les forces extérieures subies par la bille.

2.2. Etablir le travail de ces forces entre $A$ et $B$.
 
2.3. En déduire l’expression de la vitesse en $B$.

Calculer sa valeur numérique $v_{B}$.

2.4. La bille parcourt la partie rectiligne horizontale $BC =80cm$ puis arrive en $D$ avec la vitesse $v_{D} =4m/s$.

Après avoir décrit le mouvement de la bille entre $B$ et $C$, calculer la longueur $L$ de la piste $CD.  α=45^{°}$.

EXERCICE 10

Un skieur de masse $m = 80kg$ glisse sur une piste formée de trois parties :

-une partie $AB$ rectiligne incliné d’un angle $\alpha = 30°$ par rapport à l’horizontal et de longueur $L$;

-une partie $BC$ circulaire de centre $O$ et de rayon $r$ qui intercepte un angle $\beta = 60°$;

-une partie $CD$ rectiligne horizontal de longueur $L’$.

Toute la trajectoire a lieu dans un même plan vertical et le skieur part en $A$ sans vitesse initiale.

 
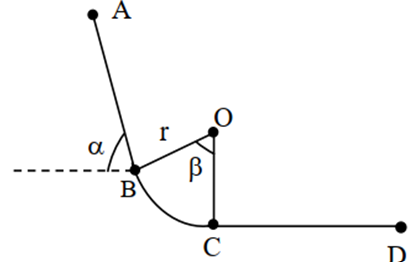
1. Les frottements sont supposés négligeables sur toute la piste.

1.1. En appliquant le théorème de l’énergie cinétique, exprimer la vitesse $V_{B}$ en fonction de $g, L$ et $\alpha$ puis la
vitesse $V_{C}$ en fonction de $g, r, L, \alpha$ et $\beta$.

1.2. Faire l’application numérique de $V_{B}$ et de $V_{C}$.

On donne : $g = 10N/kg ; L = 2,5 m$ et $r = 2,4 m$.

2. Les frottements ne sont plus négligés et ils sont équivalents à une force unique d’intensité $f$.

2.1. Exprimer les nouvelles vitesses $V_{B’}$ et $V_{C’}$ respectivement en fonction de $g, L, α$ et $f$ et en fonction de $g, r, L, β$ et $f$.

2.2. Faire l’application numérique avec les mêmes données précédentes et $f =10N$.

2.3. Le skieur arrivera-t-il en $D$ ? Justifier votre réponse clairement.

On donne $L’=100m$.

EXERCICE 11

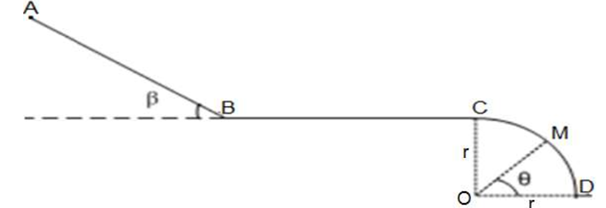
Un skieur aborde une piste constituée de trois parties (voir figure).

Le skieur, de masse  m=80kg, part du point $A$ à une vitesse V_{A}= 3m.s^{-1}$.

On donne : $g= 10N.kg^{-1}$

1- La première partie $AB$, de longueur $AB= 4m$, est un plan incliné d’angle $β = 30° $sur l’horizontal.

Les frottements sont négligeables sur la partie $AB$.
 
1.1. Faire le bilan et représenter les forces qui s’exercent sur le skieur sur la partie $AB$.

 
1.2. En appliquant le théorème de l’énergie cinétique entre $A$ et $B$, montré que la vitesse du skieur en $B$ est  $V_{B}= 7m.s^{-1}$

2. La partie $BC$, horizontale, de $BC = 8cm$ ; les frottements sont équivalents à une force d’intensité $f=120N$

2.1. Calculer sur la partie $BC$, le travail de la force de frottement $\vec{f}$

2.2. En appliquant le théorème de l’énergie cinétique entre $B$ et $C$, calculer la vitesse $V_{C}$ du skieur en $C$.
3. La partie $CD$, est un arc de cercle de centre O et de rayon  $r= 2,4m$.

Les frottements sont négligeables sur la partie $CD$.

La position de point $M$ est repéré par l’angle $\theta = (\vec{OD},\vec{OM})$

3.1. Exprimer sa vitesse $V_{M}$  du skieur au point $M$ en fonction de l’angle $\theta$, le rayon $r$ et $V_{C}$

3.2. Calculer l’angle $\theta$ pour que la vitesse du skieur au point $M$ soit  $V_{M}= 7m.s^{-1}$

EXERCICE 12

Un solide de masse $m = 1 kg$ assimilable à un point matériel glisse sur une piste formée de trois parties
$AB, BC $et $CD$ qui sont dans un même plan vertical.

-$AB$ représente un arc de cercle de centre $O$ et de rayon $r = 15 cm$.

Le point $O$ est situé sur la verticale de $B$ ;

- $BC$ est une partie rectiligne de longueur $L = 50cm $;

-$CD$ est un plan incliné de pente $8%$

Le solide est lancé en $A$ avec une vitesse initiale telle que $V_{A} = 3m/s$.

1. Énoncer le théorème de l’énergie cinétique

2. On néglige les frottements sur la partie $AB$.

Calculer la vitesse au point $B$ défini par l’angle $α = 60°$

3. Sur tout le trajet ABC existent, en fait, des forces de frottement assimilables à une force unique supposée constante, tangente à la trajectoire.

Calculer la valeur de ces forces de frottement si le solide arrive en $C$ avec une vitesse de $2,5 m/s$.

4. Arrivé en $C$ avec une vitesse de $2,5m/s$, le solide aborde la parie $CD$ et rencontre l’extrémité libre $E$ d’un ressort de constante de raideur $k$ et le comprime d’une longueur maximale$ EF = x = 3 cm$.

Seule sur la partie $CE = d =15 cm$ s’exercent des forces de frottement assimilables à une force unique $f ’$, tangente à la trajectoire, et de valeur $1N$.
 
Au-delà de $E$ on néglige les frottements.
 
Déterminer la valeur de la constante de raideur $k$ du ressort.

EXERCICE 13

Un chariot $(S)$ de masse $m = 50 g$, se déplace sur une piste rectiligne inclinée d’un angle $\alpha =10°$ par rapport à l’horizontale.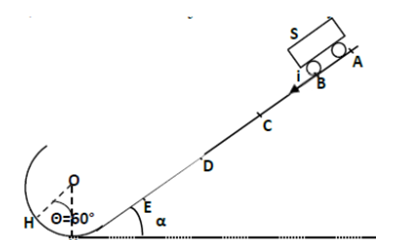

Le chariot $(S)$ est lâché sans vitesse initiale du point $A$ d’abscisse $x_{A}$ définie relativement au repère d’espace $(B,)$.

Arrivé au point $K$ avec une vitesse $v_{K}$, le chariot suit un trajet circulaire de rayon $r =0,1m$ et de centre $O$.

1. Les frottements auxquels est soumis le chariot $(S)$, au cours de son mouvement entre les points $A$ et $K$, sont équivalents à une force $f$ d’intensité supposée constante.      

A l’aide d’un dispositif approprié, on détermine la vitesse instantanée du chariot $(S)$ lors de son passage par les points $B, C, D, E$ et $K$ d’abscisses respectives $0 ; 0,2 ; 0,4; 0,6$ et $0,8 m$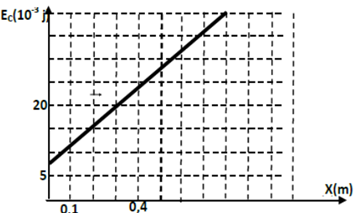

Ceci permet de tracer le diagramme de la figure ci-dessous correspondant à l’énergie cinétique du chariot $(S)$ en fonction de l’abscisse $x$ de son centre de gravité $G$.

1.1. En appliquant ce théorème au chariot $(S)$ entre la position $B$ et une position quelconque $M$ d’abscisse $x$ par rapport au repère $(B, i)$, montrer que : $Ec(x) = (mgsinα - f)x + Ec (B)$.

1.2. En exploitant le diagramme, déterminer l’intensité de la force de frottement $f$ et la valeur de l’abscisse $x_{A}$ du point $A$
     
1.3. Déterminer la valeur de la vitesse $vK$ au point $K$.

2. On supposera tout type de frottement négligeable.

2.1. Représenter les forces qui s’exercent sur le chariot.

2.2. En appliquant le théorème d’énergie cinétique montrer que : $V_{K^{2}} - V_{H^{2}} = 2gr (1-cosθ)$