EXERCICE 1

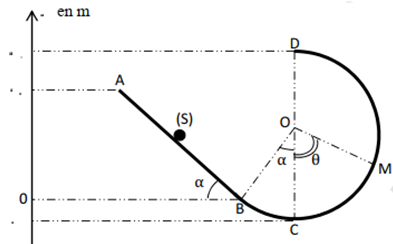
Le solide $(S)$ de masse m évolue sur la piste $ABCMD$ schématisé ci-dessous.

$AB$ est une partie rectiligne de longueur l et BD est une portion circulaire de rayon $r$.

Sur les parties $AB, BC$ et $CM$ existent les forces de frottement représentées par la force unique $\vec{f}$, d’intensité constante $f$, qui s’oppose au mouvement de $(S)$.

Données numériques : $l = 1,5m ; r = 80 cm ; α = 30° ; θ = 60° ; Z_{A}= 75cm ; Z_{B}= 149,3cm $;

vitesse de $(S)$ en $A : V_{A} = 8,6m/s $;

vitesse de $(S)$ en $B : V_{B} = 7,68m/s$

Intensité de pesanteur : $g = 10N/kg$.

Masse du solide $(S) : m = 100g$

 
3.1. Déterminer l’énergie potentielle du solide $(S)$ en $A, B, C$ et $D$.

3.2. Utiliser le théorème de la non conservation de l’énergie mécanique pour déterminer la vitesse du solide $(S)$ lors de son passage en $C$ et en $D$.

3.3. Etablir, en fonction de $V_{B}, f, r, α$ et $θ$, l’expression de la vitesse $V_{M}$ du solide $(S)$ au point $M$ en utilisant le théorème de la non conservation de l’énergie mécanique

EXERCICE 2

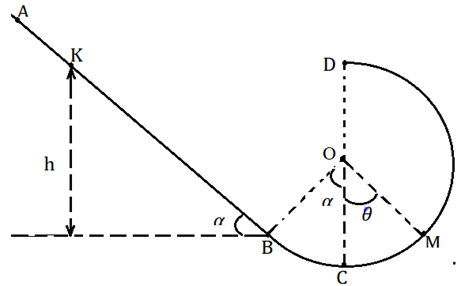
La figure ci-dessous est celle de la piste du jeu de chariot. Elle est constituée d’une partie circulaire
$BCD$ de centre $O$ et de rayon $r = 20cm$ raccordée tangentiellement en $B$ à une partie rectiligne $AB$.

Un essai consiste à lâcher, sans vitesse initiale, d’un point $K$ situé entre $A$ et $B$, à une distance $AK = x$, un petit chariot supposé ponctuel de masse $m = 1600g$.

Le jeu est gagné si le chariot rebrousse chemin au point $M$ de la partie circulaire à une hauteur $h_{2}$ qui fait la moitié de $h_{1}$.

Les forces de frottement d’intensité $f = IN$ s’exercent seulement sur la partie circulaire.

 On prendra l’énergie potentielle du chariot nulle sur l’horizontal passant par $C$.

- $\alpha =\pi/6 ; \theta = \pi/3$

- $AB = l = 1m ; g = 10N/kg$
 
1. Enoncer le théorème de la non conservation de l’énergie mécanique

2. Déterminer les énergies potentielles de pesanteur et mécaniques du chariot lors de son passage aux points  $K, B ; C, M$ et $D$

3.1. En utilisant le théorème de la non-conservation de l’énergie mécanique, montrer que la hauteur $h_{2}$ dont remonte le chariot avant de rebrousser chemin sur la partie $BCD$ a pour expression :
$h_{2} = (l - x) \sin \alpha + (1 - \cos \alpha) -\dfrac{(fr(θ+α) )}{mg} $

2.2. Déterminer la valeur de $x$ pour que le jeu soit gagné

EXERCICE 3

Une boule pleine homogène sphérique de masse $m_{1}$ er de rayon $r$ est soudée en $A$ à une tige cylindrique mince homogène $AO$ de longueur $L$ et de masse $m_{2}$.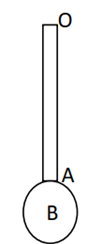

L’ensemble est mobile autour d’un axe horizontal passant par l’extrémité libre $O$ de la tige. Le système formé par la boule et la tige constitue un pendule pesant.

On écarte le pendule d’un angle $β = 60°$ à partir de sa position d’équilibre stable et on le lâche avec une vitesse angulaire $w_{o} = 5 rad/s$ (début du mouvement).
On donne $m_{1} = 0,6 kg ; m_{2} = 2/3m_{1} ; r =4 cm ; L = 15r$.

$g = 10N/kg$.
 
La position de référence de l’énergie potentielle et l’origine des altitudes sont confondues avec le point $O$     

1. Montrer que le moment d’inertie du pendule par rapport à l’axe passant par le point $O$ vaut $J =\dfrac{4596}{15}m_{1}r^{2}$ puis calculer sa valeur.

2. Déterminer l’énergie potentielle du pendule au début du mouvement.

3. Déduire l’énergie mécanique du pendule

EXERCICE 4

Le schéma de la figure $(1)$ ci-contre représente un système mécanique formé par :

-Une poulie homogène de rayon $r=20cm$ mobile autour d’un axe $(Δ)$ fixe et horizontal passant par son centre d’inertie. Son moment d’inertie par rapport à cet axe est : $J_{Δ}=2.310 kg.m^{2}$.

-Un solide $(S)$ de masse $m=400g$ attaché à l’extrémité d’un fil inextensible et de masse négligeable, enroulé sur la gorge de la poulie. Le fil ne glisse par sur la poulie.

Le solide $(S)$ repose sur un plan incliné d’un angle $α=30°$ par rapport à l’horizontale.

Lorsqu’on libère le système, le centre d’inertie $G$ du solide $(S)$ passe par le point $A$ dont la cote sur l’axe vertical $Oz$ est $z_{A}=125cm$, il glisse sans frottement sur la ligne de plus grande pente du plan incliné et passe par le point C de cote $z_{c}=45cm$ à la vitesse $v_{c}=3m.s^{-1}$

Sur la figure $(2)$, on représente les variations de l’énergie mécanique Em du solide $(S)$ en fonction de la cote z du centre d’inertie G de $(S)$.

On donne $g=10N.kg^{-1}$

Exprimer à l’aide de la figure $(2)$, l’expression de l’énergie mécanique de $(S)$ en fonction de la cote $z$.

En posant   (trouver $a$ et $b$).

1.2. Vérifier que l’énergie $E_{m}$ de $(S)$ au point $C$ vaut $3J$

1.3. Exprimer l’énergie potentielle de $(S)$ au point $C$ en fonction d’Em $(C), m$ et $vc$.

Calculer $Epp(C)$.

1.4. Déterminer la constante de l’état de référence de l’énergie potentielle de pesanteur, sachant que $c≠0$ et la position de l’état de référence de l’énergie potentielle de pesanteur $z_{0}$ sachant que $z_{0}≠0$.

1.5.Établir en utilisant la variation de l’énergie mécanique entre $A$ et $C$ que l’expression de la tension de fil $T = \alpha\sin \alpha$ et calculer sa valeur. (En utilisant $∆E_{m} ≠ 0$ et $E_{m}(Z_{A})=aZ_{}+b$ et $E_{m}(Z_{c)=aZ_{c}+b$

1.6. En appliquant le théorème de l’énergie cinétique au solide (S) entre les positions $A$ et $C$, trouver l’expression de la vitesse $v_{A}$ en fonction de $v_{c}, m, g, α, T, z_{A}$ et $z_{c}$.

Calculer sa valeur.

2. Les frottements dus à l’axe de rotation $(Δ)$ sont équivalents à un couple de moment constant $M_{c}$

2.1. En appliquant le théorème de l’énergie cinétique à la poulie entre les instants $t_{A}$ et $t_{C}$,

Trouver l’expression de $M_{c}$ en fonction de $J_{Δ}, r, v_{c}, v_{A}, α, T, z_{A}$ et $z_{c}$.

 Calculer sa valeur.
 
2.2. Le fil se détache à l’instant où le centre d’inertie G de $(S)$ passe par le point $C$.

La poulie continue à tourner et s’arrête après avoir effectué $n$ tours supplémentaires.
 
En appliquant le théorème de l’énergie cinétique, établir l’expression de $n$ en fonction   $M_{c}, J_{Δ}, r$ et $v_{c}$.
Calculer sa valeur.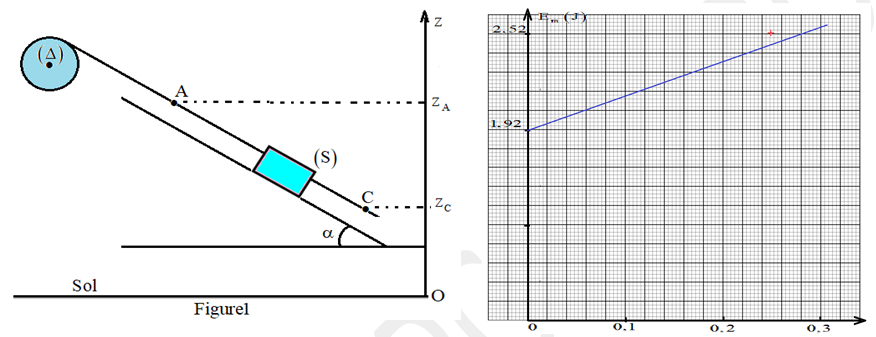

EXERCICE 5

Une boule $B$ de masse $m$, accrochée un fil inextensible de longueur $l$, est écartée de sa position d’équilibre d’un angle α et est abandonnée sans vitesse initiale.

A son passage par la position verticale, la boule percute un corps ponctuel $A$ de même masse et s’arrête.

Le corps $A$ glisse sur une piste $OCD$ (voir figure ci-dessous).

La partie $OC = d$ est un plan horizontal rugueux de coefficient de frottement dynamique $µd$ (c’est-à dire que la force de frottement sur la portion $OC$ a pour intensité $f=µdmg$).

La portion $CD = L,$ parfaitement lisse, est inclinée d’un angle $β = 30°$ par rapport l’horizontale.

1. Donner l’expression de la vitesse de la boule $B$ juste avant de toucher le corps $A$

2. En utilisant le théorème de l’énergie cinétique, exprimer la vitesse du corps $A$ après l’interaction.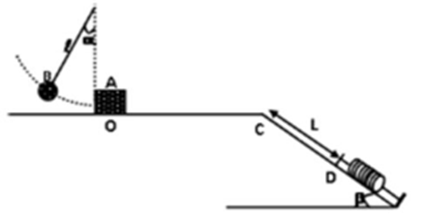

3. 1. Représenter les forces exercées sur le corps $A$ en une position entre $O$ et $C$.
 
3.2. En appliquant le théorème de l’énergie cinétique, exprimer la vitesse du corps $A$ au point $C$ en fonction de $g, l, d, α$ et $µd$.
     
3.3. De quel angle $αm$ doit-on écarter la boule $B$ pour que le corps $A$ arrive en $C$ avec une vitesse nulle.

4. A partir du point $C$, le corps A aborde la partie $CD$ avec une vitesse nulle.
 
Il arrive sur un ressort parfait de longueur à vide l0 et de constante de raideur $k$.
 
4.1. En appliquant la conservation de l’énergie mécanique, montrer que : $\dfrac{1}{2}kx^{2} – (mgsinβ)x-mgL\sinβ=0x$ étant la valeur de la compression maximale du ressort
 
NB : On pourra considérer le plan horizontal passant par $C$ comme référence de l’énergie potentielle de pesanteur.

4.2. En déduire la valeur de la compression maximale du ressort.

On donne : $m=200g ; l=100cm, d=1m, µd=0.1, g=10N/kg, k=140N/m$

EXERCICE 6

Une bille de masse $m=500g$ et de dimensions négligeable est lancé à un point $A$ avec une vitesse

Elle se déplace sur glissière constituée de trois parties :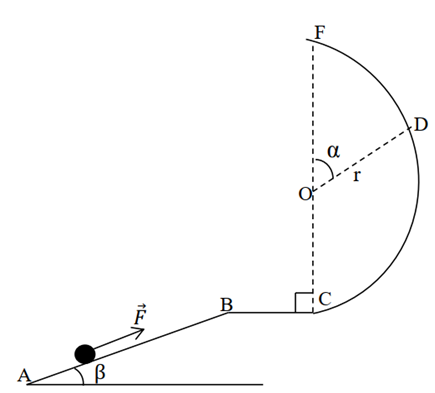

une rectiligne $AB=2m$ incliné de $β=30°$ sur l’horizontal, une partie horizontal $BC$ et une partie circulaire $CF$ de centre $O$ et rayon $r=50cm$.

Une force constante de valeur $F=4,5N$ agit sur la bille uniquement sur la partie $AB$.

Le plan horizontal passant par $B$ est la référence des énergies potentielles de pesanteur

Le point $D$ est repéré par angle $α=60°$

L’énergie mécanique du système bille-terre au point $C$ vaut $Em_{C}=5J$.

Les frottements sont négligeables

1. Calculer l’énergie potentielle du système bille-terre en $A$      

2. Calculer la vitesse de la bille en $A$
 
3. Calculer la vitesse de la bille en $D$

EXERCICE 7

Une bille assimilable à un point matériel de masse $m=200g$ est relié à un point fixe $O$ (Voir figure)
On $θ_{0}=600 ; l=1,6m$

La bille est lancée vers le bas avec une vitesse initiale $V_{0}= 3m.s^{-1}$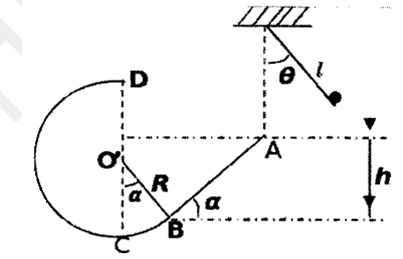

A  une date quelconque, la position de la bille est repérée par l’angle $θ$ que forme le fil avec la position d’équilibre

1. Exprimer la vitesse de la bille en fonction $V_{0}, g, l, θ $et $θ_{0}$

2. On suppose que la corde se casse lorsque la bille passe par la verticale de $A$.     
 
Elle aborde à la vitesse $V_{A}=5m.s^{-1}$ une piste oblique et une partie circulaire $BCD$ raccordé tangentiellement en $B$ à $AB$, de rayon $R=25cm$
 
2.1. Calculer l’énergie mécanique de la bille en$ A$.

On donne : $AB=1m$ et $α=450$
 
2.2. En supposant que les frottements sont négligeables, quelle sera la vitesse de la bille en $D$ ?

2.3. En réalité, on constate qu’en $D$, la bille n’a que la moitié de la vitesse précédente

Cela est dû aux pertes d’énergie mécanique du fait de l’existence des forces de frottements correspondant à une force constante $\vec{f}$ qui exerce sur la bille entre $A$ et $D$

Calculer $f$

EXERCICE 8

Ali s’amuse avec son jouet (solide $(S)$ de masse $m$) dans une gouttière $ABCD$.

Ce jouet peut glisser sans frottement dans la gouttière.

La portion AB est inclinée d’un angle $α =30°$ sur l’horizontale, la portion $BC$ est horizontale, et la portion $CD$ est un quart de cercle de rayon $R$ et de centre $O$.

Le solide $(S)$ passe au point $A$ avec une vitesse $V_{A}= 3 m/s$.

On note $E_{A}$ et $E_{B}$ respectivement l’énergie mécanique du système Terre-solide aux points $A$ et $B$, on note $V_{B}$ la vitesse du solide en $B$.
On donne : $AB=d=6m ; m=24kg ; g=10N/kg$.

On choisit comme niveau de référence pour énergie potentielle de pesanteur, le plan horizontal contenant le tronçon horizontal $BC$

1. Exprimer, puis calculer numériquement $E_{A}$.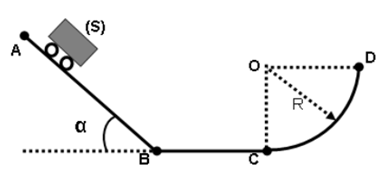

2. En appliquant le théorème de l’énergie cinétique entre les positions $A$ et $B$, exprimé V_{B}$ en fonction de $V_{A}, d, α$, et $g$.

Puis calculer numériquement $V_{B}$.

3. Exprimer, puis calculer numériquement $E_{B}$.

4. Comparer $E_{A}$ et $E_{B}$.

Le résultat était-il prévisible ? Justifier votre réponse.     
 
5. En appliquant le théorème de l’énergie cinétique entre les positions $C$ et $D$, établir une relation entre $V_{B}, R$ et $g$, si on admet que le solide $(S)$ parcours le tronçon $BC$ à vitesse constante et arrive en D avec une vitesse nulle.
 
Calculer numériquement $R$.

EXERCICE 9  

Un service au tennis

Au service, un joueur de tennis frappe, à l’instant de date $= 0 s$, une balle de masse $m = 58,0 g$ à une hauteur $h = 2,4 m$ au-dessus du sol et lui communique alors une vitesse de valeur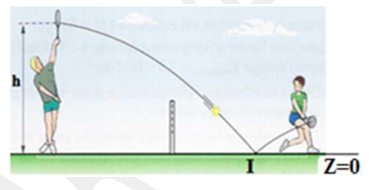

La balle décrit une trajectoire parabolique, et touche le sol au point $I$ On négligera les frottements.

Dans le référentiel terrestre, on prend pour référence d’énergie potentielle l’altitude du terrain $EPP= 0 J$, et l’intensité de la pesanteur : $g = 9,81 N/kg     $

1. Calculer l’énergie cinétique $E_{C}(t_{0})$ et l’énergie potentielle de pesanteur $EPP (t_{0})$ de la balle à l’instant de  date $t_{0}$

2. Donner l’expression de l’énergie mécanique $E_{m} (t_{0})$  de la balle cet instant $t_{0}$, puis calculer sa valeur

3. Que vaut l’énergie potentielle de pesanteur à l’instant $t_{1}$ où la balle touche le terrain en $I$ ?

4. Rappeler le principe de conservation de l’énergie mécanique, et déduire des questions précédentes la valeur de l’énergie cinétique de la balle puis sa vitesse à la date $t_{1}$.

Justifier.

5. En réalité la vitesse d’impact au point $I$ est-elle inférieure, supérieure ou égale à la valeur calculée à la question précédente ? Justifier

EXERCICE 10

Un solide $(S)$ supposé ponctuel, de masse $m=100g$ est lancé à partir d’un point $A$, avec une vitesse initiale lancé à partir d’un point $A$, avec une vitesse initiale $V_{A}=4m.s^{-1}$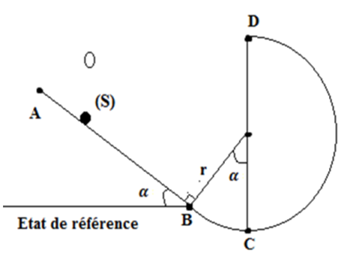

Il glisse à l’intérieur d’une piste $ABCD$ constituée de deux parties :

- Une partie rectiligne $AB$, de longueur $AB=80 cm$, et inclinée d’un
$Angle α=30 °$ par rapport au plan horizontal.

- Une partie circulaire $BCD$ ($CD$ verticale) de rayon $r= 35cm$ et de centre $O$.

On choisit le plan horizontal passant par le point $B$ comme état de référence de l’énergie potentielle de pesanteur $E_{PP}$     

1. On néglige tous les frottements sur la partie $ABC$.

1.1. Ecrire l’expression de $E_{PP} (A)$  de $(S)$ au point A.

Calculer sa valeur.

1.2. En déduire la valeur de l’énergie mécanique $E_{M} (A)$ de $(S)$ au même point $A$.

1.3. Ecrire l’expression de $E_{PP}(C) $de $(S)$ au point $C$, Calculer sa valeur

1.4. Sachant que l’énergie mécanique de $(S)$ se conserve sur la partie $ABC$.

Calculer l’énergie cinétique $E_{C}(C)$ puis la vitesse $V_{c}$ au passage au point $C$.
1.5. Soit $F$ un point de la partie $AB$ où $E_{C}(F)=7E_{PP}(F)$.  

Calculer l’énergie potentielle puis la distance $d=AF$

2. L’énergie mécanique de $(S)$ au passage en $D$ devient $E_{m}(D)=19000114J$

2.1. Montrer qu’il existe des forces de frottements dans la piste $CD$

2.2. Calculer la variation $∆E_{M}$ de l’énergie mécanique de $(S)$ entre les pointes $C$ et $D$, que devient cette énergie dégradée d’énergie mécanique

2.3. Ecrire l’expression de $∆E_{M}$ en fonction du travail de la réaction de la piste sur $(S)$, déduire l’intensité de la force équivalente aux frottements entre $(S)$ et la piste $CD$.

EXERCICE 11

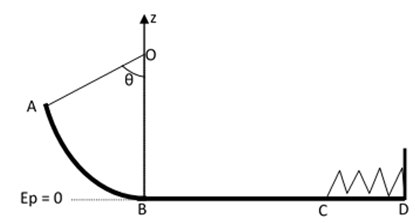
Un solide assimilable à un point matériel, de masse $m = 100 g$, glisse sur une piste formée de trois parties $AB,  BC$ et $CD$.

La partie $AB$ est $arc$ de cercle de rayon $R = 5 m$ et de centre $O, BC$ est une partie rectiligne horizontale de longueur $l = 5 m$ et $CD$ est une partie rectiligne lisse.

On donne $θ = 30°$.

3.1. Calculer l’énergie potentielle de pesanteur du solide aux points $A, B$ et $C$.

On choisira l’état de référence des énergies potentielles le plan horizontal passant par $B, C $et $D$ ; et l’origine des altitudes en $B$.

3.2. Le solide part de $A$ sans vitesse initiale.
 
3.2.1. Calculer son énergie mécanique en $A$.

3.2.2. Que devient cette énergie en $B$ si les frottements sont négligeables ?

3.2.3. Calculer alors dans ces conditions, la vitesse du solide en $B$ et $C$.

3.3. En réalité sur le plan $BC$, il existe des forces de frottement d’intensité constante $f$.  

Ainsi, le solide arrive en $C$ avec une vitesse $V_{C} = 1,66 m/s$.

Calculer alors l’intensité des forces de frottement.

3.4. En $C$, est placé horizontalement un ressort de raideur $K = 100 N/m$ dont l’extrémité libre coïncide avec le point $C$ et l’autre extrémité étant fixe en $D$.

Calculer la compression maximale $x_{0}$ du ressort.

EXERCICE 12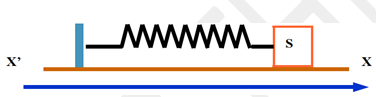

1. Une masse $m = 150g$ est accrochée à un ressort

Ce ressort est étiré de $x_{m} = 10,0 cm$, puis lâché sans vitesse initiale.

Pendant le mouvement de va et vient, la vitesse maximale atteinte par la masse $m$ vaut $v_{m} = ± 4,00 m/s$.

Il n’y a pas de frottements.

1.1. Que peut-on dire de l’énergie mécanique de ce système ?

1.2. Avec ces informations, calculer la valeur numérique de cette énergie mécanique $E_{m}$

1.3. Déterminer la raideur k du ressort

2. Quand le ressort est comprimé de $x_{1}$, la masse m possède une vitesse dont la valeur algébrique vaut $v_{1} = + 1,50 m/s$.

Il n’y a pas de frottements.
2.1. Où se situe le solide S par rapport à la position d’équilibre du ressort et dans quel sens se déplace-t-il ?

2.2. Donner l’expression littérale de $x_{1}$ en fonction de $E_{m}, v_{1}$ et $m$.

Calculer numériquement $x_{1}$

3. Alors que le solide passe par la position d’équilibre en se déplaçant vers la droite, un dispositif permet de décrocher la masse : à partir de cet instant, le ressort n’a alors plus aucune action sur le solide $S$

3.1. Quelle est la valeur numérique $v_{2}$ de la vitesse à cet instant précis ?

3.2. Quelle sera le mouvement de la masse en supposant qu’il n’y a pas de frottements.

Justifier votre réponse

3.3. En réalité, au moment où la masse se décroche, elle est soumise tout le long de son mouvement à une force de frottements dont l’intensité vaut $f$
Sachant que la masse s’arrête au bout d’une distance $d = 1,5m$, calculer l’intensité f de cette force

EXERCICE 13

Un pendule élastique est constitué par un solide ponctuel $(S)$ de masse $m= 400g$ qui  est relié à un ressort de masse négligeable et de raideur $k= 14,4N/m$. L’ensemble est posé sur un plan incliné d’un $angle = 30°$ par rapport à l’horizontale.

Sur ce plan les frottements sont  suposés négligeables.

1. Trouver l’allongement $x_{0}$ du resort à l’équilibre.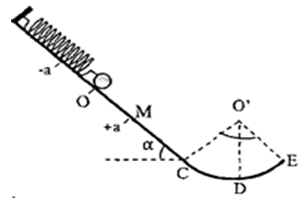

2. On écarte le solide $(S)$ d’une distance $a= 6cm$ vers le bas et le lâche sans vitesse initiale.

Le pendule oscille entre $x= +a $et $x= -a$.

2.1. Donner l’expression de l’énergie potentielle quand le solide est au point $x= +a$ en fonction de $k, x_{0}$ et $a$.

Faire l’application numérique.

2.2. Exprimer la valeur V de la vitesse de passage du solide $(S)$ au point $O$ (position d’équilibre) en fonction de $k, m$ et $a$.

Calculer $V$.     

-L’état de référence des énergies potentielles de pesanteur est choisi à la position d’équilibre.

-L’état de référence des énergies potentielles élastiques est choisi pour le ressort détendu.

3. Après plusieurs oscillations le solide se détache du ressort au pont $M$ d’abscisse $x= +a$.

Le solide glisse sur la piste $MCDE$ formé de deux parties :

-Une partie rectiligne $MC$ lisse de longueur $L= 6,4cm$;

-Une partie circulaire $CDE$ de centre $O’$, de rayon $r= 8cm$ et d’angle au centre $β= 60°$.

3.1- Déterminer, de deux manières différentes, la valeur $V_{C}$ du solide au point $C$.

3.2- Le solide arrive en $D$ avec une vitesse de valeur $V_{D}= 0,9m/s$.

a- Calculer les variations de l’énergie potentielle $ΔE_{pp}$ et l’énergie cinétique $ΔE_{C}$ entre $C$ et $D$.

b- Les forces de contact exercées par la piste $CDE$ sur le solide sont-elles conservatives ?

Justifier.

 Si non, déterminer l’intensité supposée constante de la force non conservative