EXERCICE 1

On considère deux particules élémentaires de même masse $m$ environ $2000$ fois plus petite que celle d’un nucléon, l’une de charge électrique $q_{A}$ et l’autre de charge $q_{B}$ telle que $q_{B} = - q_{A}$, placées respectivement en $A$ et $B$ ; avec $AB = d = 750 pm$.

Donnée : $k = 9,0.109 SI$

1. A l’aide du schéma ci-dessous, définir le signe de chacune de ces charges en détaillant les explications

 
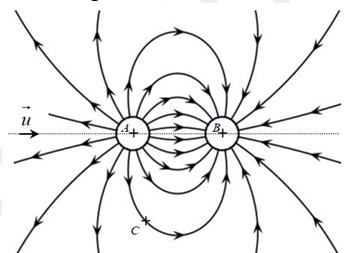
2. Le champ électrostatique est-il uniforme aux alentours du point $B$ ?

Justifier votre réponse. Aucun calcul n’est demandé.

3. Sachant que$ |q_{A}| = |q_{B}| = e = 1,60.10-19 C$, définir la nature probable de chacune de ces deux particules élémentaires.

4. Tracer ci-dessus, sans tenir compte de sa norme, le vecteur champ électrostatique $\vec{E}$ généré par ces deux particules au point $C$.

5. Donner l’expression de la valeur $F$ de la force électrostatique exercée par la particule $A$ sur la particule $B$ en fonction de e, d et de la constante électrique $k$.

Calculer cette valeur $F$

EXERCICE 2

Pour déterminer l’intensité du champ électrique créé entre deux plaques parallèles et horizontales, on utilise le dispositif ci-contre constitué d’un ressort de raideur $k=100 N/m $et fixé à la plaque supérieure par l’intermédiaire d’un isolant.

À son extrémité libre, on suspend une petite bille de masse m et de charge $q=6 10^{-7} C$.

Un générateur crée entre les deux plaques un champ électrique uniforme.

- Lorsque la plaque supérieure est reliée au pôle positif du générateur, le ressort s’allonge de $Δl1 =2,5 cm$

- Lorsqu’elle est reliée au pôle négatif, le ressort s’allonge de $Δl2=1,3 cm$.

 
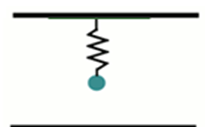
1. Faire le bilan des forces exercées sur la bille et schématiser la situation dans chaque cas.

2. Déterminer l’intensité du champ électrique entre les deux plaques

EXERCICE 3

1. Quelle est l’intensité de la force exercée sur la charge de $5,0 μC$ indiquée ci-dessous ?

 
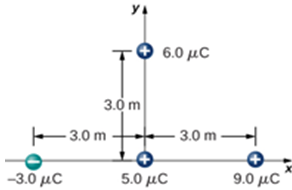
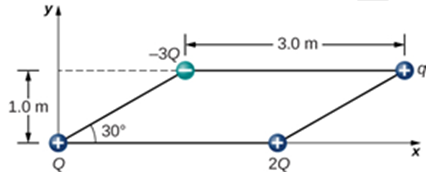
2. Quatre particules chargées sont positionnées aux angles d'un parallélogramme, comme indiqué ci-dessous.

Quelle est la valeur de la force nette sur $q$?

On donne : $q=5.0μC$ et $Q=8.0μC$,

 
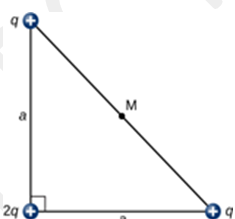
3. Quel est l’intensité du champ électrique au point médian $M$ de l'hypoténuse du triangle illustré ci-dessous?

 
4. Trouver la valeur du champ électrostatique à P pour les configurations de charge indiquées ci-dessous.  

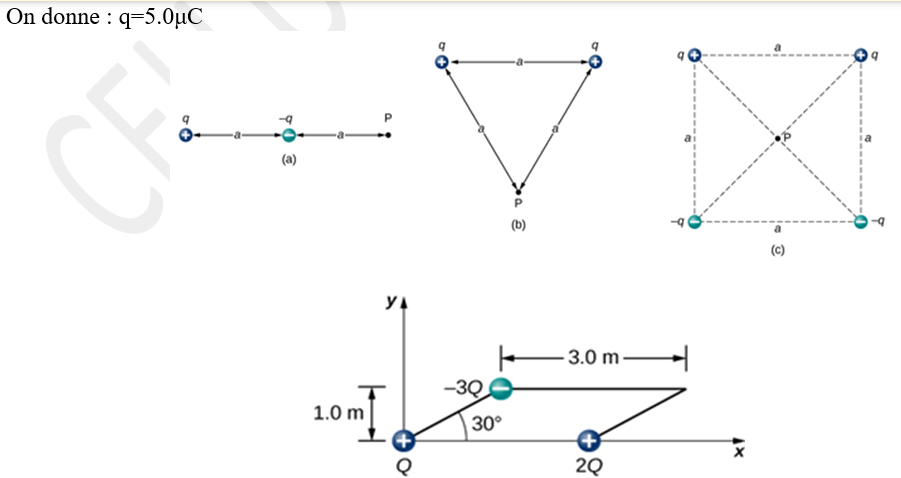
On donne : $q=5.0μC$

EXERCICE 4

On considère trois charges $q_{1}, q_{2}$ et $q_{3}$ situées aux sommets d’un triangle équilatéral de côté $r = 4 cm$.

On donne : $q_{1} = 3.10^{-8} C, q2 = -3.10^{-8} C$ et $q_{3} = 3.10^{-8} C$. $k = 9.109 u S.I$.

1. Calculer les valeurs des deux forces électriques qui s’exercent sur la charge q1, dues à la présence des charges $q_{2}$ et$ q_{3}$.

2 1. Déterminer

graphiquement une valeur approximative de la force équivalente exercée sur la charge $q_{1}$.

2.2. Retrouver cette valeur par le calcul.

EXERCICE 5

Entre le proton et l’électron d’un atome d’hydrogène existe une interaction électrique.

a. Cette interaction est-elle attractive ou répulsive ?

b. Représenter les forces électriques qui s’exercent entre le proton et l’électron ;

c. Calculer la valeur de la force électrique exercée sur l’électron ; la comparer à son poids, en supposant que l’électron se trouve à une distance moyenne $r = 0,5.10^{-10} m$ du noyau.
Données :

-charge élémentaire $e = 1,6.10^{-19} C $

-masse de l’électron $m_{e} = 9,1.10^{-31} kg$

-masse du proton $m_{p}=1,67.10^{-27}kg$

-intensité de la pesanteur $g=9,81N.kg-^{1}$

EXERCICE 6

Deux corps électrisés, supposés ponctuels, portent deux charges identiques de valeur $q = 2.10^{-8} C$.

Ils sont placés en deux points $A$ et $B$ distants de $d = 6 cm$.

En un point $P$ de la médiatrice du segment $AB$, on place une autre charge $q’ = 10^{-8} C$.

1. Représenter la force électrique équivalente s’exerçant sur la charge $q’$.

2. Calculer sa valeur sachant que les points $A, B$ et $P$ formant un triangle équilatéral.

3. Prouver qu’il existe un point $M$ de la médiatrice de $[A, B]$, tel que la force électrique équivalente est nulle. Préciser $M$

EXERCICE 7

Deux petites sphères, chacune de masse $m = 0,30 g$ et de charge $Q$, sont accrochées chacune à l'extrémité inférieure d'un fil de longueur $l = 20cm$ dont l'extrémité supérieure est accrochée au même point fixe $O$.

A l'équilibre, les fils font entre eux un angle $θ = 8°$.

1. Faire le bilan des forces qui s'exercent sur une sphère.

2. Ecrire la condition d'équilibre pour une sphère supposée ponctuelle.

3. En déduire la valeur de la force de Coulomb qui s'exerce sur une sphère.

4. Calculer la valeur de la charge portée par une sphère.

5. L'angle θ varie-t-il linéairement avec la charge électrostatique portée par les sphères

Donnée: $k = 9.10^{9} u S.I$.

EXERCICE 8

Un pendule électrique est constitué d’une boule très légère de masse $m = 0,1g$ portant une charge positive $q = 10^{-8} C$, suspendue à un fil de longueur  l = 0,2 $m$.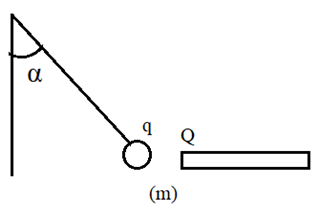

En approchant un bâton d’ébonite portant une charge $Q$, le pendule dévie ; le fil prend une inclinaison $α = 20°$ avec la verticale et la boule s’approche du bâton.

1. Préciser, en justifiant la réponse, le signe de la charge $Q$ portée par le bâton.     

2. Représenter les forces qui s’exercent sur la boule.

3. Déterminer la valeur de la force électrique exercée par le bâton d’ébonite sur la boule.

4. En admettant que la charge $Q$ est localisée à l’extrémité du bâton, à une distance $r = 2 cm$ de la boule, trouver $Q$.

On donne : $g=9,8N.kg^{-1}$

EXERCICE 9

Un ensemble de quatre charges électriques ponctuelles $+q, - q, +2q $et$ -q$ placées respectivement en $A, B, C$ et $D$ sommets d’un carré de côté $a = 4 cm$.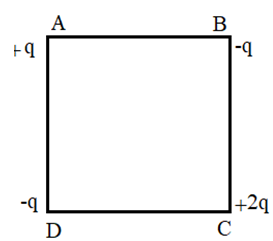

1. Déterminer les caractéristiques des trois forces électriques s’appliquant sur la charge en $A$.

On donne $q = 10^{-9} C$.

2. Faire une représentation de ces forces à l’échelle ;

3. Trouver, graphiquement et par le calcul, la force équivalente appliquée en $A$.

Comparer les valeurs trouvées. 

EXERCICE 10  

Une charge ponctuelle $q = 2.10^{-6} C$ est placée en un point $M$ où règne un champ électrique créé par une autre charge $Q_{0}$.

Elle est alors soumise à une force électrique horizontale, dirigée vers la gauche et de valeur $F=6.10^{-3}N$

1. Préciser les caractéristiques du vecteur champ électrique au point $M$.

2. Représenter et en adoptant l'échelle suivante :

$1cm$ représente $10^{-3} N ;  1cm$ représente $10^{3} N.C^{-1}$

3. Quel est le signe de $Q_{0}$, sachant qu’elle se trouve à droite de la charge $q$ ?

EXERCICE 11

Un pendule électrique, dont la boule a une masse $m = 0,1 g$, portant une charge q, est placé dans une région de l'espace où se trouve une charge ponctuelle $Q = 2.10^{-8}C$.

1. En approchant la charge $Q$ du pendule, on constate que l'inclinaison à l’équilibre du pendule augmente.

Expliquer le phénomène.

2. L'inclinaison du pendule à l’équilibre correspond à un angle $α =10°$, comme l'indique la figure ci-contre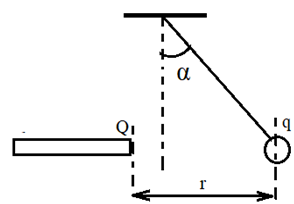

- Déterminer le signe de $q$.

- Quelle est la valeur de la force électrique à laquelle est soumis le pendule ?

3. Sachant que $q = 3.10^{-8}C$, quelle est la valeur du vecteur champ électrique en ce point ?    
 
4. En utilisant la loi de Coulomb, retrouver la valeur de pour une distance $r = 17,7cm$ séparant les deux charges.

On donne : $g=9,8N.kg^{-1}$

EXERCICE 12

Une première charge ponctuelle crée en un point A un vecteur champ électrique de valeur $15.10^{5} N.C^{-1}$, une deuxième charge ponctuelle crée au même point $A$ un champ électrique de vecteur de valeur égale à $20.10^{5} N.C^{–1}$.

Sachant que $\vec{E_{_1}}$ et $\vec{E_{_2}}$ sont orthogonaux :

1. trouver la valeur du vecteur champ électrique résultant ;

2. faire une construction à l’échelle et retrouver graphiquement le même résultat ;

3. quelle est la valeur de la force électrique à laquelle est soumise une particule de charge $q = 10^{– 6} C$ placée en $A$ ?

EXERCICE 13

Une particule chargée supposée ponctuelle de masse me et portant une charge$ (-e)$, est maintenue immobile dans le champ de pesanteur grâce à un champ électrique uniforme de vecteur $\vec{E}$

Déterminer les caractéristiques de $\vec{E}$

On donne : $e = 1,6.10^{–19} C$ et $m_{e} = 9,1.10^{–31} kg ; g=9,8N.kg^{-1}$

EXERCICE 14

Une goutte d’huile électrisée négativement est introduite entre deux plaques métalliques parallèles et horizontales $A$ et $B$ entre lesquelles règne un champ électrique de vecteur $\vec{E}$dont la valeur est réglable.

1. Représenter les forces qui agissent sur la goutte d’huile.

2.1. Indiquer laquelle des deux plaques est liée à la borne positive, pour que la goutte puisse s’immobiliser dans le champ électrique sachant que $A$ est la plaque supérieure.

2.2. En déduire la valeur de la charge $q$ portée par la goutte.

On donne $= 18,75.10^{3} N.C^{–1} ; g=10 N.kg^{–1} $; masse de la goutte $m = 0,3.10^{–10} kg$

EXERCICE 15

En deux points $A$ et $B$, on place respectivement les deux charges électriques q et $q’$.

Soit $O$ le milieu du segment $AB$.

La charge $q = 10 μC$ placée en $A$ crée en $O$ le champ électrique d’intensité $E_{A}=9.10^{9}N.C^{–1}$

Déterminer l’intensité du vecteur champ électrique en $O$ lorsque :

1. $q’ = q = 10 μC$.

2. $q’ = - q = -10 μC$.

EXERCICE 16

Il existe dans une région de l’espace $D$, deux champs électriques uniformes de vecteurs et orthogonaux de valeurs $E_{1}= 3.10^{4} N.C^{–1}$ et $E_{2}= 4.10^{4} N.C^{–1}$
 
Une charge électrique $q = 2μC$ est placée dans un point de l'espace $D$.

1 Quelle est la valeur de la force électrique à laquelle est soumise la charge $q$?

2. Calculer en degrés, la valeur de l’angle α entre les directions du vecteur champ $\vec{E_{_1}}$ et de la force  $\vec{F}$

EXERCICE 17

Des gouttes d’huile électrisées peuvent se déplacer entre deux plaques métalliques horizontales et distantes de $1cm$ ou règne un champ électrique de vecteur

L’une des gouttes s’immobilise lorsque $E= 3,5.10^{4} N.C^{–1}$, la plaque de dessus étant chargée positivement.

Déterminer la charge de la goutte et la comparer à la charge élémentaire $e$.

On donne : masse de la goutte $m = 2,24.10^{-15}kg ; g= 10 N.kg^{-1}$ et $e = 1,6.10^{-19} C$.

EXERCICE 18

Une boule sphérique de centre $C$ est attachée au point $O$ par un fil isolant de masse négligeable et de longueur $l = 40 cm$.

La boule de masse $m = 0,05g$ porte la charge électrique $q$.

1. On la soumet à un champ électrique uniforme, horizontal, orienté vers la droite et d’intensité
$E = 10^{3} V.m^{-1}$.

Le fil s’incline alors d’un angle $α = 10°$ par rapport à la verticale.

En déduire la valeur de la charge électrique $q$.

2. On superpose au champ électrique précédent un autre champ électrique uniforme de vecteur horizontal.

Quels doivent être le sens et l’intensité de $\vec{E}$, pour que le fil s’incline de $α’ = 20°$ par rapport à la verticale ?

3. Quelle serait l’inclinaison $α”$ du fil si l’on changerait le sens de $\vec{E}$,sans modifier son intensité ?

EXERCICE 19

Deux charges ponctuelles $q_{1} = 10nC$ et $q_{2} = 40nC$ sont placées respectivement en deux points $A$ et $B$ distants de $a = 30 cm$.

1. Déterminer les caractéristiques du vecteur champ électrique au milieu $O$ du segment $AB$.

2. Il existe sur la ligne joignant les deux points $A$ et $B$, un point $M$ où les deux champs électriques se compensent.

2.1. Indiquer, sur la droite $(AB)$, s’il est plus proche de $A$ ou de $B$.

2.2. Calculer la distance $AM$

EXERCICE 20

Soit le dipôle $AB$, défini dans le repère $(O, x, y)$. Les points $A, B$ et $M$ ont pour coordonnées : $A (-a, 0)$ et $B (a, 0)$ et $B (0, r)$

1. Donner au point M, les caractéristiques du champ $\vec{E}(A/M)$ créé par la charge $–q$ puis celles du champ $\vec{E}(B/M)$ crée par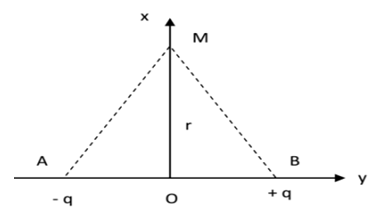
$+q$ : (les intensités seront données en fonction de $q, a$ et $r$).

2. Déterminer en fonction de $q, r$ et a les coordonnées du vecteur champ résultant :

2.1. Au point $O$ milieu de $[AB]$.    
 
2.2. Au point de la médiatrice de $[AB]$.

2.3. Que devient l’intensité du champ en $M$ lorsque $OM$ est très grand devant $AB$