EXERCICE 1

1.1. Schématiser la pile associée à l'équation chimique : $Zn + Pb^{2+}\rightarrow Pb + Zn^{2+}$

1.2. Donner le symbole de la pile étudiée.

2. Une mesure de la $f.é.m$. de cette pile donne E = + 0,63 V lorsque $[Zn^{2+}] = [Pb^{2+}]$.

2.1. Préciser la polarité des bornes et le sens de circulation du courant dans le circuit extérieur.

2.2. Quelles sont les transformations qui ont lieu dans chaque compartiment ?

Quelle est la réaction chimique qui se produit quand la pile débite du courant ?

EXERCICE 2

On considère la pile symbolisée par : $Sn | Sn^{2+}|| Co^{2+}| Co$.

1.1. Représenter avec toutes les indications utiles cette pile par un schéma.

1.2. Ecrire l'équation chimique associée à cette pile.

2. Une mesure de la $f.é.m$. nous permet de déduire que la borne positive est la borne de gauche.

2.1. Préciser le signe de la $f.é.m$.

2.2. Déterminer le sens de circulation du courant dans le circuit extérieur quand la pile débite du courant.

2.3. Déduire l'équation chimique qui symbolise la réaction qui se produit spontanément quand la pile débite du courant.

EXERCICE 3

1. Si on plonge un fil de cuivre dans une solution d'acide chlorhydrique à $pH$ nul, on n'observe pas de réaction.

Dans les mêmes conditions un fil de plomb donne lieu à un dégagement de dihydrogène.

1.1. Ecrire l'équation de la réaction qui s'est produite.

1.2. Classer les corps simples $Pb, Cu$ et $H_{2}$ par pouvoir réducteur croissant.

2. 1. Déduire du résultat précédent, quel sera le pôle positif de la pile suivante :
$Cu | Cu^{2+} || Pb^{2+} |Pb$.

2.2. Ecrire l'équation de la réaction redox spontanée qui se produit quand la pile débite du courant et schématiser la pile en indiquant le sens du courant et des électrons.

2.3. Ecrire l'équation de la réaction associée à cette pile. Déduire le signe de la $ f.é.m$. de cette pile.

EXERCICE 4

De la grenaille métallique de zinc de masse $m=0,56g$ réagit avec une solution d'acide chlorhydrique de concentration $C=5mol/L$.

1. Ecrire les formules des couples mis en jeux.

2. Ecrire les demi-équations correspondantes.

3. Etablir l'équation de la réaction d'oxydoréduction.

4. Calculer la quantité de matière initiale de zinc

5.1. Quel est le volume nécessaire de la solution d'acide chlorhydrique pour faire disparaitre complètement la grenaille de zinc?

5.2. Quel est le gaz formé au cours de cette transformation?

5.3. Quel est le volume du gaz dégagé à la fin de la réaction, sachant que le volume molaire $V_{M}=25L/mol$

5.4. Décrire une méthode opératoire permettant de mesurer le volume du gaz échappé.

EXERCICE 5

On veut déterminer la composition massique d’un échantillon de cupronickel (alliage cuivre-nickel) en l’attaquant par un excès d’une solution d’acide chlorhydrique.

Suite à cette attaque le nickel $Ni$ est oxydé en ion nickel $Ni^{2+}$ et il se dégage du dihydrogène $H_{2}

1. Ecrire les demi équations électroniques traduisant les transformations subies par le nickel $Ni$ et l’ion $H3O^{+}$.

2. En déduire l’équation bilan de la réaction d’oxydoréduction qui a eu lieu. Préciser l’oxydant et le réducteur.

3. Préciser les couples oxydant-réducteur mis en jeu au cours de cette réaction.

4. L’attaque d’un échantillon de masse m égale à $5,0 g$ donne un volume $V$ égal à $381,6 cm^{3}$ de dihydrogène, mesuré dans les conditions où le volume molaire $V_{M}$ est égal à $22,4L.mol^{-1}$.

4.1. Déterminer la masse m’ de nickel dans l’échantillon.

4.2.  En déduire le pourcentage massique du nickel dans l’alliage cuivre-nickel utilisé.

4.3. Choisir parmi les formulations données ci-dessous celle qui convient à cet alliage.

Donnée : Selon le pourcentage massique du nickel, les alliages cuivre-nickel peuvent avoir l’une des formulations suivantes : $CuNi 5, CuNi 20$ ou $CuNi 25$

EXERCICE 6

Une pile Daniell ($1836$, physicien anglais)$ Zn/Zn^{2+}// Cu^{2+}/Cu$ débite pendant $24h$ un courant  d’intensité
$I = 15 mA$.

1. Calculer la quantité d’électricité $(Q)$ transférée en $24h$, en ampèreheures et en coulombs.

En déduire la quantité de matière d’électrons  libérée par l’anode.

2. Calculer la quantité de métal :

2.1. Qui disparaît sur l’électrode (anode) de zinc $(n_{Zn})$.

2.2. Qui apparaît sur l’électrode (cathode) de cuivre $(n_{Cu})$.

3. En déduire la variation de masse de chaque électrode, $m_{Zn}$ et $m_{Cu}$.

4. Etablir la relation : $m=\dfrac{1}{2}\dfrac{ItM}{F}$

EXERCICE 7

On dispose d’une électrode standard à hydrogène, d’une électrode d’argent et d’une électrode de zinc.

En couplant l’électrode à hydrogène et l’électrode d’argent on obtient une pile de $0,8V$ de $f.é.m$., le pôle + étant l’argent.

En couplant l’électrode d’argent et l’électrode de zinc on obtient une pile de $1,56V$ de $f.é.m$., le pôle + étant l’argent.

1. Qu’appelle-t-on électrode standard à hydrogène ?

2..Quel sera le potentiel d’électrode attribué à l’électrode d’argent ?

À l’électrode de zinc ?

3. On considère la pile $Zn/ Zn^{2+} //Ag^{+}/ Ag$

3.1. Qu’appelle-t-on anode ?

Écrire la demi-équation redox à l’anode.

3.2. Qu’appelle-t-on cathode ?

Écrire la demi-équation redox à la cathode.

4. On fait débiter la pile.

4.1. Ecrire sa réaction de fonctionnement.

4.2. Préciser sur un schéma le sens du courant, l’anode, la cathode et les polarités de la pile.

EXERCICE 8

Le zinc et le cuivre sont parfois utilisés en tôle pour la couverture des immeubles.

En milieu industriel les pluies acides peuvent être très acides et il a été établi, dans une zone où la pluie a un $pH$ égal à $3$, que la masse $m$ de zinc attaqué est donnée par la relation :
$m = K.S.t$ dans laquelle :

- $K = 3,3.10^{-2} kg.m^{-2}.an^{-1}$ est le coefficient d’attaque spécifique du métal,

- $S$ est l’aire, en $m_{2}$, de la pièce métallique soumise à l’action des pluies,
 
 - $t$ est la durée d’exposition en années.

Données : $ρ_{Zn} = 6860 kg.m^{-3} ; M(Zn) = 65,4g.mol^{-1}
E^{0}Zn^{2+}/Zn= -0,76V ;  E0Cu^{2+}/Cu = 0,34V$ et $E0H_{3O^{+}}H_{2} = 0V$

1. Expliquer pourquoi le zinc est attaqué par les pluies acides et dire si le cuivre l’est également.

2. Sachant que seule la face externe est soumise à l’action des pluies, calculer :

2.1. La perte de masse annuelle d’une plaque de zinc d’épaisseur $e = 1,0mm$, de longueur $L= 2,00m$ et de largeur $l = 0,25m$.

2.2. La perte d’épaisseur en un an.

2.3. La durée de vie maximale d’une tôle.

3.1. Ecrire l’équation de la réaction entre les ions hydronium et le zinc.

3.2. Calculer la quantité d’ions hydronium (en moles), qui réagit en un an avec la tôle de zinc.

3.3. En déduire le volume d’eau de pluie ayant réagi avec le zinc en un an

EXERCICE 9

Pour protéger une canalisation en fonte (alliage à base de fer $Fe$) enterrée dans le sol, de la corrosion, on la relie à une électrode de magnésium $(Mg)$ de masse $m = 10 kg$, elle aussi enterrée.

1. Ecrire la réaction qui a lieu sur le magnésium, montrer que la canalisation est protégée contre les agressions oxydantes.

Le courant de corrosion dans le fil de plomb qui relie la canalisation à l’électrode de magnésium a une intensité $I=60mA$.

2. Après avoir calculé la quantité de magnésium oxydé $(n_{Mg})$, la quantité d’électrons ($ne^{-}$) libérée par l’anode, la quantité d’électricité $(Q)$ transférée, calculer la durée de vie « théorique » $(t)$ de l’électrode de magnésium. $(F ≈ 96500C.mol^{-1})$.

3. Etablir la relation : $t=2 \dfrac{mF}{IM}$

4. Peut-on remplacer le magnésium par du plomb $Pb$ ?

EXERCICE 10

Données :

-Masses atomiques molaires: $M(Zn)= 65g·mol^{–1} ; M(Cu) =63,5g·mol^{–1}$

- Potentiels standard d'oxydo-réduction : $Cu^{2+}/Cu : 0,34V ;  H_{3}O^{+}/H_{2} : 0V ; Zn^{2+}/Zn : – 0,76V$

-Constante des gaz parfaits : $R = 8,314J·mol^{–1}·K^{–1}$,

-$T = θ +273$.

On souhaite déterminer la teneur en zinc d'un échantillon de tombac, laiton formé d'un alliage de cuivre et de zinc.

On prélève une masse $m = 5,0g$ de cet alliage finement broyé, et on le place dans une solution d'acide chlorhydrique en excès.

Un gaz se dégage qu'on recueille sur la cuve à eau. On mesure son volume $V = 0,55L$, alors que la pression est $P= 101 000 Pa$ et la température $θ = 19°C$.

1. Montrer que la quantité de matière du gaz formé vaut sensiblement $n = 23 millimoles$.

2. Pourquoi met-on « une solution d'acide chlorhydrique en excès » ?

3. Le cuivre et le zinc sont-ils attaqués par l'acide ? Justifier la réponse.

4. Ecrire l'équation de la réaction entre le métal attaqué et l'ion hydronium.

5. Déterminer la quantité de matière $n'$ (en moles) du métal qui a réagi ainsi que sa masse $m'$.

6. Calculer la teneur « $τ$ » en zinc de l'alliage.

EXERCICE 11

On sait que le fer est sensible à la corrosion.

On examine quelques-unes de ses propriétés.

1. Le fer est attaqué par les solutions aqueuses acides.

En présence d'une solution d'acide chlorhydrique diluée ($pH$ de l'ordre de $3$ ou $4$), il apparaît des ions
$(Fer II)$ (On notera ces ions : $Fe^{2+})$ et du dihydrogène $H_{2}$

1.1. Ecrire les demi-équations d'oxydo-réduction correspondant aux transformations du fer en ion $(fer II)$ et de l'ion en $H^{+}$ en dihydrogène $H_{2}$

1.2. En déduire l'équation chimique traduisant l'attaque du fer par une solution acide.

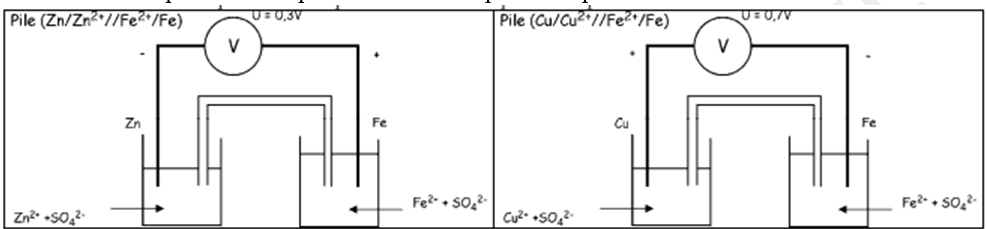
2. Le zinc $Zn$ et le cuivre Cu sont deux métaux susceptibles de donner respectivement les ions $Zn^{2+}$ et $Cu^{2+}$.

On suppose que l'on se place dans des conditions telles que le fer ne peut donner que l'ion ($fer II$).

2.1. On construit les piles $(Zn / Zn^{2+} // Fe^{2+} / Fe) et (Fe / Fe2+// Cu^{2+}, / Cu)$.

Les montages correspondants sont représentés ci-dessus.

Dans le premier cas, on lit une tension $U = 0,3V$, le zinc étant le pôle négatif.

Dans le deuxième, on lit $U = 0,7V$, le fer étant le pôle négatif.

Que prouvent ces deux expériences ?

Ecrire les demi-équations électroniques qui ont lieu aux électrodes en précisant bien le sens.

Ecrire les équations représentant les réactions chimiques qui ont lieu quand les piles commencent à débiter, c'est-à-dire juste après qu'on ait remplacé le voltmètre par une lampe.

2.2. Un appareil comme un bateau (ou un tracteur) a une coque en acier susceptible de rester en milieu très humide.

On admet que l'humidité ambiante joue le rôle des électrolytes (solutions de sulfate de fer, de zinc ou de cuivre) et que l'acier se comporte comme le fer.

On veut protéger l'appareil.

Va-t-on choisir comme électrode un morceau de zinc ou un morceau de cuivre ? Pourquoi ?

Que faut-il faire régulièrement ?

3. On sait que le fer est également protégé lorsqu'il est en milieu très basique ($pH$ compris entre $10$ et $13$).

On veut renforcer le caractère basique des bétons qui le sont déjà.

Quel produit envisageriez-vous d'incorporer au ciment afin que l'armature en acier des bétons armés ne soit pas attaquée?

EXERCICE 12

Un moyen de protéger les canalisations souterraines en fer consiste à raccorder celles-ci à des blocs de zinc qu'on sacrifie et qu'on remplace régulièrement.

La réalisation de cette protection peut être schématisée par la figure ci-dessous :

 
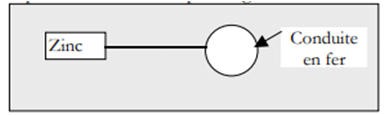
La rouille qui se forme sur la canalisation est formée en partie avec des ions fer $II (Fe^{2+}$).

Le but de la protection est de reformer du fer sous sa forme métal.

Le zinc sacrifié se transforme lors de la réaction en ion zinc $II (Zn^{2+})$.

1. Compléter les demi-équations électroniques proposées ci-dessous sur la feuille réponse
$Fe^{2}→ Fe
Zn → Zn^{2+}$

Puis écrire l'équation bilan de cette réaction sur la même feuille réponse.

2. Indiquer le sens de déplacement des électrons dans la jonction fer zinc en complétant la figure de la feuille réponse $n°l$.

Indiquer le pôle positif et le pôle négatif de la pile en court-circuit ainsi réalisée.

3. Le courant circulant dans cette jonction est de 50 mA

Quelle quantité d'électricité ce courant transporte-t-il par jour ?

Quelle masse de zinc est de cette façon sacrifiée par jour ?

4. Citer un autre moyen de lutte contre la corrosion.
Données

- $M(Zn) = 65,4g·mol^{–1}$

- La charge portée par une mole d'électrons est: $Qmol = 96500 C$.

- La quantité d'électricité transportée par un courant d'intensité $I$ pendant une durée $∆t$ est donnée par l'expression suivante : $Q = I.∆t$

EXERCICE 13   Protection d'un ballon d'acier

« Les ballons d'eau chaude sont en acier, ils sont pourvus sur toute leur surface interne d'une couche protectrice en émail.

Elle est apposée à l'aide d'un procédé spécial et garantit, avec l'anode de magnésium (un oxydant) incorporée en supplément, une protection efficace contre la ………..

L'anode de magnésium est à faire contrôler une première fois au bout de $2 ans$ puis à intervalles correspondants par le service après-vente et éventuellement à remplacer.

En fonction de la qualité de l'eau potable (conductivité électrique) il est conseillé de faire contrôler l'anode à intervalles plus courts.

Si le diamètre de l'anode se réduit à des valeurs de l'ordre de 10 à $15mm$, il est recommandé de la remplacer ».

1. Le mot caché dans le texte est un phénomène lié aux réactions d'oxydoréduction. Lequel ?

2. La rouille est un exemple de ce phénomène. Expliquer succinctement l'origine de la rouille.

3. L'acier est susceptible de produire de la rouille, en déduire son composant majoritaire.

4. Définir les termes en gras dans le texte.

5. Ecrire les équations de demi-réactions correspondantes aux couples redox donnés.

6. D'après les deux questions précédentes, déduire le sens de la réaction ayant lieu à l'anode.

7. Justifier ainsi les valeurs des potentiels électrochimiques donnés pour les deux couples.

Au bout d'un an, on constate que le diamètre de l'anode cylindrique est égal à $23mm$.

8. Calculer la masse initiale, puis la masse finale (après $1 an$), de l'anode de magnésium.

9. En déduire la masse m de magnésium a été « consommée » en une année.

10. A l'aide de l'équation de la demi-réaction ayant lieu à l'anode, et de la question précédente, calculer la quantité de matière d'électrons émis en $1 an$.

11. En déduire la quantité d'électricité $Q$ qui a circulé à travers l'anode en une année.

12. On suppose que l'intensité I du courant qui traverse l'anode est constante.

Calculer la valeur de I en ampère.

Données :
Longueur initiale de l'anode en magnésium :$ L = 200 mm$ ; diamètre :$ d = 33mm$.

Magnésium : symbole : Mg ; masse volumique : $ρ = 1738 kg.m^{-3}$ ; masse molaire : $M = 24g.mol^{-1}$

Charge élémentaire : $e = 1,6.10^{-19} C$ ;

Nombre d'Avogadro : $Na = 6,02. 1023 mol^{-1} $;

Quantité d'électricité transportée par une mole d'électrons : 1 faraday $(F) = 96 485 C$

Une année $= 365,25$ jours
Couples redox :
$Mg^{2+}/Mg : E^{0} = -2.37 V
Fe^{2+}/Fe : E^{0} = -0.44 V$

EXERCICE 14

Une poudre métallique finement broyée de masse $m = 16,5 g$ contient du zinc, du cuivre et de l’aluminium de masses respectives $m_{1}, m_{2}$ et $m_{3}$.

Cette poudre est attaquée par un excès d’une solution d’acide chlorhydrique.

Après réaction il reste un résidu solide de masse égale à $3,5 g et le gaz dégagé occupe dans les conditions de l’expérience un volume de $11,2L$.

1. Utiliser la classification électrochimique de la figure $12$ pour identifier le résidu et les métaux qui passent en solution et les cations correspondants.

2. Ecrire les équations bilans des réactions redox qui ont eu lieu.

3. Calculer les masses $m_{1}, m_{2}$ et $m_{3}$.

4. En déduire la composition centésimale massique de la poudre métallique.

EXERCICE 15

On donne ci-dessous la classification électrochimique suivante:    

 
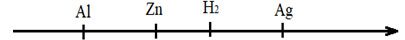
1. Prévoir ce qui peut se produire quand on plonge respectivement :

1.1. Une lame d’aluminium dans une solution aqueuse de nitrate de zinc $Zn(NO_{3})_{2}$ ;

1.2. Une lame d’argent dans une solution aqueuse de nitrate d’aluminium $Al(NO_{3})_{3}$.

Ecrire quand cela est possible l’équation chimique de la réaction qui a lieu.

2. Sachant que le zinc est attaqué par les ions plomb $Pb^{2+}$ et que le plomb réagit avec une solution aqueuse d’acide chlorhydrique avec dégagement de dihydrogène :

2.1. Écrire l’équation chimique de la réaction observée ;

2.2. Déterminer la place du plomb dans la classification proposée.

3. Une lame d’aluminium de masse $m = 5,40g$ est introduite dans une solution aqueuse de nitrate d’argent de volume $V = 100cm^{3}$ et de concentration molaire $C = 1mol.L^{-1}$.

3.1. Qu’observe-t-on ?

3.2. Ecrire l’équation chimique de la réaction observée.

3.3. Montrer que l’aluminium $Al$ est en excès par rapport aux ions argent Ag+.

d) Calculer la masse de la lame d’aluminium et la concentration de l’ion $Al^{3+}$ lorsque la réaction est terminée.

Donnée : La masse molaire atomique en $g.mol^{-1}$ est $Al = 27$

EXERCICE 16

On réalise une pile avec les couples $Fe^{2+}/Fe$ et $Ag^{+}/Ag$ Sachant que les potentiels standards d’oxydoréduction sont : $E^{0} (Fe^{2+}/Fe) =-0.44 V$ et $E^{0} (Ag^{+}/Ag) =0.80 V$

1. Faire le schéma de la pile débitant dans un résistor et un ampèremètre ; on indiquera : sa polarité, le sens du courant et des électrons.

2. Quel rôle joue le pont salin dans une pile ?

3. Donner la représentation conventionnelle de cette pile.

4. Écrire les équations des réactions aux électrodes lorsque la pile fonctionne.

En déduire l’équation-bilan dans la réaction naturelle entre les couples.

5. Quel est l’oxydant ?

Le réducteur ?

A quelle borne
y’a oxydation ? Réduction ?

6. Calculer la $f.é.m$. de la pile. Les solutions étant à $1mol/ L$

7. La pile fonctionne pendant $5h$, produit un courant $I=0.2A$.

On constate que la masse d’une des électrodes à augmenter de $m$.

On donne $1F=96500C M(Ag)= 108g/mol, M(Fe)=56g/mol$

7.1. De quelle électrode s’agit-il ?

7.2. Calculer la masse m

EXERCICE17  Pile argent-zinc

On s’intéresse à la pile schématisée par $Ag(s)|Ag+(c) et Zn^{2+}(c′)|Zn(s)$ avec $c = 0,18 mol·L^{−1$ et
$c′ = 0,30 mol·L^{−1}$.

Le compartiment de gauche a un volume $V = 100 mL$, celui de droite un volume $V ′ = 250 mL$.

Données : $E^{◦} (Zn^{2+}/Zn) = −0,76 V et E^{◦}(Ag^{+}/Ag) = +0,80 V$

1. Déterminer la $f.é.m$. de la pile. Identifier alors l’anode et la cathode.

2. Écrire les réactions électrochimiques aux électrodes puis la réaction de fonctionnement qui se produit lorsque la pile débite.

3. Schématiser le déplacement des porteurs de charge dans chaque partie de la pile lorsqu’elle débite du courant.

4. Déterminer la composition de la pile lorsqu’elle est usée. Quelle quantité d’électricité, en coulombs, a-t-elle débité ?