EXERCICE 1

On considère la pile Leclanché constituée par les couples redox $Zn^{2+}/Zn$ et $MnO_{2}/MnO_{2}H$.

L'électrolyte est une solution de chlorure d'ammonium où la quantité d'ions hydronium est égale à $10^{-4} mol$.

1. La solution d'électrolyte est-elle acide ? Neutre ? Ou basique ?

2. Ecrire l'équation chimique qui se produit pendant la décharge de cette pile.

3. 1. En admettant que la plaque de zinc qui enveloppe la pile est de $0,01 mm$ d'épaisseur, de $4cm$ de longueur et de $1cm$ de largeur dites lequel des réactifs $Z_{n}$ ou $H_{3}O^{+}$ n'est pas en excès en admettant que le dioxyde de manganèse est en grand excès par rapport à ces deux entités.

3.2. La plaque de zinc peut-elle se perforer dans ces conditions ?

On donne la masse volumique du zinc : $ρ_{Zn} = 7,14 g.cm^{-3}$

EXERCICE 2

On met une masse $m=2,12g$ du cuivre métallique dans un ballon contenant un volume $V=250mL$ d’acide nitrique $(H^{+} +NO_{3}^{-})$ de concentration $C=0,2mol/L$ et la solution prend progressivement une coloration bleue avec dégagement du mono oxyde d’azote $NO$ incolore.

1. Quelles sont les précautions qu’on doit prendre pendant cette expérience ?

2. A quoi est due la coloration bleue qui apparait ?

3. Ecrire les demi-équations puis en déduire l’équation bilan de la réaction qui se produit.

4. Déterminer le volume du gaz $NO$ qui se dégage à la fin de la réaction dans les conditions suivantes
$(20o C ,1bar)$.

On donne :$ M(Cu)= 63,5g/mol ،R=8,314(S.I)$

EXERCICE 3

Le couple $MnO_{4}/Mn^{2+}$ participe à une réaction dans laquelle l'eau oxygénée $H_{2}O_{2}$ se transforme en dioxygène $O_{2}$ gazeux.

1. Ecrire l'équation d'oxydoréduction.

2. Y'a-t-il oxydation ou réduction de l'eau oxygénée? Justifier votre réponse.

3. On ajoute de l'eau oxygénée à une solution aqueuse contenant des ions iodure $I^{-}$
 La coloration de la solution montre l'existence du diiode $I_{2}$

3.1. L’eau oxygénée est-elle oxydant ou réducteur dans cette réaction? Justifier
votre réponse.

3.2. Sachant que les couples mis en jeux dans cette réaction sont : $I_{2}/I^{-} ; H_{2}O_{2}/H_{2}O$, écrire l'équation de la réaction d'oxydoréduction.

EXERCICE 4

A $10 mL$ d’eau de javel contenant $6.10^{-2} mol$ d’ion hypochlorite $ClO^{-}$, on ajoute une solution d’iodure de potassium $KI$ contenant $8.10^{-2} mol$ d’ion iodure $I^{-}$.

A ce mélange on ajoute quelques gouttes d’une solution d’acide sulfurique; on observe alors une coloration brune suite à la formation du diiode $I_{2}$.

1. L’un des couples redox mis en jeu dans cette expérience est le couple $ClO^{-}/Cl^{-}$.

Préciser l’autre couple redox.

2. Etablir l’équation formelle associée à chaque couple redox.

3. En déduire l’équation bilan de la réaction d’oxydoréduction.

Justifier l’ajout de l’acide sulfurique.

4. Déterminer la quantité de matière de diiode $I_{2}$ formé

EXERCICE 5

Une poudre métallique finement broyée de masse $m = 16,5g$ contient du zinc, du cuivre et de l’aluminium de masses respectives $m_{1}, m_{2}$ et $m_{3}$.

Cette poudre est attaquée par un excès d’une solution d’acide chlorhydrique.

Après réaction il reste un résidu solide de masse égale à $3,5g$ et le gaz dégagé occupe dans les conditions de l’expérience un volume de $11,2 L$.

1. Utiliser la classification électrochimique pour identifier le résidu et les métaux qui passent en solution et les cations correspondants.

2. Ecrire les équations bilans des réactions redox qui ont eu lieu.

3. Calculer les masses $m_{1}, m_{2}$ et $m_{3}$.

4. En déduire la composition centésimale massique de la poudre métallique.

Données :

- Les couples redox à considérer sont: $Cu^{2+}/Cu, Zn^{2+}/Zn$ et $Al^{3+}/Al$.

- Les masses molaires atomiques en $g.mol^{-1}$ sont $Zn = 65,4$ et $Al = 27$.

- Dans les conditions de l’expérience le volume molaire des gaz est égal à $22,4 L.mol^{-1}$.

EXERCICE 6

Le châssis d'une fenêtre d'appartement est en aluminium.

Il peut se détériorer au contact de l'air humide
$(O_{2} + H_{2}O)$.

Les couples d'oxydoréduction mis en jeu sont :$ O_{2} / H_{2}O : E°=0,4 V ; Al^{3+}//Al : E°= -1,66 V$

1. Quel est l'oxydant le plus fort ? Justifier.

2. Ecrire la demi équation électronique concernant le couple $Al^{3+}//Al$.

- Equilibrer la demi-équation électronique concernant le couple $O_{2}/H_{2}O$ et indiquer le sens de la réaction.
$O_{2}/H_{2}O + e^{-} = HO^{-}$.

Est-ce une oxydation ou une réduction ? Justifier.

3. Justifier que l'équation bilan de la réaction d'oxydoréduction s'écrit :
$2Al + 1,5O_{2} + 3H_{2}O = 2Al^{3+}+6HO^{-}$

4. Sur l'ensemble du châssis, il s'est formé $16 g$ d'hydroxyde d'aluminium $Al (OH)3$ ; calculer la masse d'aluminium détérioré.

On donne les masses molaires suivantes : $H: 1 ; O: 16 ; Al : 27g/mol$

EXERCICE 7

1. Définitions : définir les termes suivants : oxydant, réducteur, couple redox, demi-équation électronique.

2. Ecrire les demi-équations électroniques des couples suivants : $Cu^{2+} / Cu (E^{0}=0,34V);
Cl_{2} / Cl-(E^{0}=1,36 V) ; Ag^{+} / Ag (E^{0}=0,8 V)$

3. Réactions d'oxydo-réduction :

3.1. Ecrire les équations d'oxydo-réduction entre les couples suivants :

-$Cu^{2+} / Cu$ et $Cl_{2} / Cl^{-}$

- $Ag^{+} / Ag$ et $Cu^{2+} / Cu$

3.2. Pile électrochimique : on réalise une pile électrochimique avec les couples suivants : $Ag^{+} / Ag$ et $Cu^{2+} / Cu$.

- Représenter le dispositif expérimental.

- Préciser la polarité des électrodes.

- Donner la force électromotrice de la pile

EXERCICE 8

Le Lugol® est une solution antiseptique.

Elle doit son nom au médecin français Jean Lugol ($1788-1851$).

-L’étiquette d’un flacon $100 mL$ de Lugol® précise que cette solution contient $1,0 g$ de diiode $I2$ soit une quantité de matière $n = 3,9$ mmol de diiode.

-On souhaite vérifier cette indication à l’aide d’un titrage d’un échantillon de volume $V = 10,0mL$ de Lugol® par une solution de thiosulfate de sodium $(Na^{+}+ S_{2}O_{3}^{2-})$ de concentration en quantité
$[S_{2}O_{3}^{2-}] = 100mmol.L^{-1}$.

- L’équivalence est repérée lorsqu’un volume $V_{E} = 8,4mL$ de solution titrante est versée.

Données : couples oxydant/réducteur : $I_{2} /I^{-}$ et $S_{4}O_{6}^{2-}/S_{2}
O_{3}^{2-}$

1. Démontrer à partir des couples oxydant/réducteur que l’équation support du titrage s’écrit :

$I_{2} + 2S_{2}
O_{3}^{2-}\rightarrow 2I^{-} + S_{4}O_{6}^{2-}$.

Les ions sodium $Na^{+}$ sont spectateurs.

2. Calculer la quantité $n_{E}$ (en mol) de thiosulfate de sodium versée à l’équivalence.

3. Donner une définition de l’équivalence.

4. Donner la relation entre la quantité $n_{0}(I_{2})$ en début de titrage et la quantité $n_{E}$ de thiosulfate de sodium versée à l’équivalence.
 
Calculer la quantité $n_{0}(I_{2})$ en début de titrage.

5. Seul le diiode est coloré. Comment repère-t-on l’équivalence lors de ce titrage ? Justifier rapidement.

6. A partir du titrage, calculer la quantité $n(I_{2})$ de diiode dans $100mL$ de solution de Lugol®.

Si on admet $5%$ d’erreur, la solution de Lugol® est-elle acceptable ?

Donnée éventuelle : $M(I) = 126,9g.mol^{-1}$
 

EXERCICE 9

Action de l'air humide sur un châssis de fenêtre en aluminium.

Masse atomique molaire $(g/mol) : Al : 27 ; O : 16 ; H : 1

\begin{array}{|c|c|c|}
\hline
\text{Couple oxydant / réducteur}& \text{ Potentiel standard (V)}&\text{ Demi-équation électronique}\\
\hline
O_{2}/HO^{-}    &0,4    &O_{2}+ 2H_{2}O+4e^{-}=4HO^{-}\\
\hline
Cu^{2+}/Cu&    0,34    &Cu^{2+}+2e^{-}=Cu\\
\hline
Fe^{2+}/Fe&    -0,44&    Fe^{2+}+2e-=Fe\\
\hline
Al^{3+}/Al    &-1,67&\\
\hline
\end{array} $

1. Ecrire et équilibrer la demi équation électronique du couple $Al^{3+}/Al$.

2. L'exposition de l'aluminium à l'air humide provoque une réaction chimique qui produit de l'alumine de formule $Al(OH)3$ qui soude forme ionique peut s'écrire $Al^{3+} ; 3HO^{-}$.

A l'aide des deux demi équations des couples $Al^{3+}/Al$ et $O_{2}/HO^{-}$, équilibrer l'équation bilan suivante : $Al+O_{2}+H_{2}O=Al^{3+}+3HO^{-}$.

Une masse $m=100g$ d'aluminium réagit avec le dioxygène de l'air et l'eau pour former de l'alumine. Quelle est la masse molaire de l'alumine.

- Quelle est la quantité de matière qui a réagi ?

- Quelle est la masse d'alumine formée ?

EXERCICE 10

Le fioul est un carburant utilisé pour le chauffage domestique et dans les centrales thermiques pour la production de l'électricité etc.

La teneur massique maximale légale en soufre dans le fioul est de $0,3%$.

Pour déterminer la teneur en soufre d'un fioul, on brûle complètement $100 g$ de fioul et on fait barboter les gaz de combustion, uniquement constitués de dioxyde de carbone $CO_{2}$, de dioxyde de soufre $SO_{2}$ et de vapeur d'eau, dans $500,0 mL$ d'eau.
 
On obtient une solution $(S)$ dans laquelle tout le dioxyde de soufre formé est supposé dissous.

On prélève un volume V_{Red} = $10,0mL$ de la solution $(S)$ que l'on dose avec une solution de permanganate de potassium de concentration $C_{OxU} = 0,005 mol.L^{-1}$.

On admet que seul le dioxyde de soufre est alors dosé.

L'équivalence est obtenue pour un volume versé de la solution de permanganate de potassium égal à$ V_{OxE} = 12,5mL$

1. Ecrire l'équation chimique de la réaction de dosage sachant que les couples redox mis en jeu sont :
$MnOç{4}^{-}/Mn^{2+}$ et $SO_{4}^{2-}/ SO_{2}$.
 
Préciser le rôle joué par le dioxyde de soufre.

2. Déterminer la concentration $C_{Red}$ du dioxyde de soufre dans la solution $(S)$.

3. Calculer la quantité de dioxyde de soufre dissoute dans la solution $(S)$.

4. En déduire le pourcentage massique en soufre du fioul. Ce fioul est-il conforme à la législation?
Donnée : $M(S) = 32g.mol^{-1}$

EXERCICE 11

Pour réaliser un circuit imprimé, on utilise une plaque recouverte de $20 µm$ d’épaisseur de cuivre.

Considérons alors une plaque carrée de 10 cm de côté.

1. Déterminer la masse de cuivre déposée sur cette plaque.

Le circuit imprimé représente $20 %$ de la surface de cette plaque, et pour faire disparaître les parties de la plaque qui ne correspondent pas au circuit électrique, on plonge la plaque dans un bain de $200$ mL de trichlorure de fer $III (Fe^{3+}+ 3Cl^{-})$

Ce bain a été obtenu en dissolvant 100 g de trichlorure de fer $III$ dans $1L$ d’eau.
 
$FeCl_{3}→Fe^{3+} +3Cl^{-}$

2.1. Calculer la concentration en ions fer $III$ et chlorure.

2.2. Calculer la quantité de matière d’ions fer $III$ et chlorure dans les $200mL$ (en moles).

Les potentiels dans les conditions standard des couples redox  $Cu^{2+} /Cu$ et$ Fe^{3+}/ Fe^{2+}$ sont respectivement :$ 0,34 V$ et $0,77 V$.

3.1. Donner la définition d’un oxydant, d’un réducteur, d’une oxydation et d’une réduction.

3.2. Ecrire la demi-équation électronique pour chaque couple.

3.3. Ecrire l’équation bilan qui traduit l’action du trichlorure de fer $III$ sur le cuivre.

4. Déterminer les concentrations en ions $Cl^{-} ; Cu^{2+} ; Fe^{2+}$ et $Fe^{3+}$  dans le bain en fin de réaction.

Donnée : $ρ_{Cu} = 8,9.103 kg.m^{-3}$

EXERCICE 12

Une pile alcaline zinc-dioxyde de manganèse a les caractéristiques suivantes :

- $f.é.m. = 6,0 V$

- capacité : $0,10 Ah$

- puissance maximale : $0,20 W$

Les réactions se produisent aux électrodes en zinc et en carbone entouré de $MnO_{2}$ sont :

- électrode de zinc : $Zn +4OH^{-}\rightarrow[Zn (OH) ]^{2}- + 2e^{-}$

- électrode de carbone : $MnO_{2}+ 2H_{2}O+2e-→Mn(OH)2 +2OH^{-}$

1. Sur quelle électrode se trouve la borne positive ?

2. Désigner le type de la réaction qui se produit sur chaque électrode.
3. Quelle est la quantité $Q$, exprimée en coulombs, que peut fournir la pile ?

4. Combien de temps peut-elle fonctionner à pleine puissance, la $f.é.m$. restant constante ?

En déduire l’énergie que peut fournir la pile.

5. Calculer les masses minimales de zinc et de dioxyde de manganèse que la pile doit contenir afin de pouvoir fournir toute la quantité d’électricité disponible.

Donnée : charge électrique d’une mole d’électrons en valeur absolue : $9,65.104 C.mol^{-1}$

EXERCICE 13

Après avoir introduit un volume $V_{0} = 2,00mL$ d’une solution commerciale d’hypochlorite de sodium $(Na^{+}+ClO^{−})$ dans une fiole jaugée de volume $V_{f} = 100 mL$, on complète avec de l’eau distillée jusqu’au trait de jauge.

À un volume $V = 10,0 mL$ de cette solution fille, on ajoute environ 10mL d’une solution d’iodure de potassium ($K^{+}+ I^{−}$) à $15 %$ en masse et$ 5,0 mL$ d’acide éthanoïque CH_{3}CO_{2}H à $3,0mol·L^{−1} $

L’échantillon obtenu est titré par une solution de thiosulfate de sodium ($2Na^{+} + S_{2}O_{3}^{2−}$) de concentration
$C = 2,0·10^{−2} mol·L^{−1}$.

Le volume équivalent est égal à $V’= 16,0 mL$.
 
Données : potentiels standards à $298 K
E^{◦} (ClO^{−}/Cl^{−}) = 0,89V ; E^{◦} (I2 /I−) = 0,54V$ et $E^{◦} (S_{4}O_{6}^{2−}/S_{2}O_{3}^{2−}) = 0,08 V$

1. Proposer une équation pour la réaction entre les ions hypochlorite $ClO^{–}$ et les ions iodure $I^{–}$.

Prévoir qualitativement le caractère favorisé ou défavorisé de la réaction.

2. Proposer une équation pour la réaction de titrage du diiode $I_{2}$ par les ions thiosulfate $S_{2}O_{3}^{2–}$.

Prévoir qualitativement le caractère favorisé ou défavorisé de la réaction.

3. Sachant que les ions iodure et l’acide éthanoïque sont introduits en excès, déterminer la concentration en ions hypochlorite dans la solution commerciale

EXERCICE 14  Accumulateur lithium métal

On étudie ici l’accumulateur lithium-oxyde de manganèse, qui représente environ $80 %$ du marché des batteries au lithium.

La première électrode est en dioxyde de manganèse $MnO_{2}$, la deuxième en lithium Li.

Ces deux électrodes baignent dans un électrolyte organique contenant des ions $Li^{+}$.

Données : Numéro atomique du lithium : $Z = 3$ ;

. Masse molaire du lithium : $M = 5,9g · mol^{−}1$ ;

. Potentiels standard : $E^{◦}1(Li+/Li(s)) = −3,03V et E◦2 (MnO_{2}(s)/LiMnO_{2}(s)) = 0,65V$.

1. Donner la configuration électronique du lithium.

Indiquer sa position dans le tableau périodique. Pourquoi choisir un électrolyte organique plutôt que de l’eau ?

2. Écrire les réactions aux électrodes lorsque l’accumulateur fonctionne en générateur, ainsi que la réaction globale de fonctionnement.

3. La pile contient-elle un pont salin ou équivalent ? Pourquoi ?

4. Déterminer la force électromotrice de la pile.

5. Déterminer la capacité $C$ de la pile en $A·h$ pour une masse initiale de $2g$ de lithium

EXERCICE 15

On veut vérifier la teneur en chrome d’un acier $35 CD 4$ par une méthode chimique.

Les grandes lignes du principe sont les suivantes :  

Une prise d’essai de masse m est attaquée par de l’acide sulfurique dilué : le chrome et le manganèse sont oxydés respectivement à l’état d’ions $Cr^{3+}$ et $Mn^{2+}$.

En milieu acide fort le peroxodisulfate d’ammonium ($NH_{4})2S_{2}O_{8}$, appelé encore persulfate, oxyde les ions chrome $Cr^{3+}$ en ions $Cr_{2}O_{7}^{2‐}$ et les ions $Mn^{2+}$ en ions $MnO_{4}^{‐}$, ces réactions étant catalysées par les ions argent $Ag+$

L’excès de peroxodisulfate et les ions permanganate sont alors éliminés en traitant la solution à l’ébullition par de l’acide chlorhydrique.  

La solution alors obtenue contient les ions dichromate qui peuvent être dosés par une solution de sel de $Mohr [FeSO_{4}, (NH_{4})2SO_{4}, 6H_{2}O]$ soit par une méthode directe, soit en retour.  

1. En décomposant chaque réaction en deux demi‐réactions, écrire les équations bilans des réactions suivantes en précisant les oxydations et les réductions :

‐action de l’ion péroxodisulfate $S_{2}O_{8}^{2‐}$ sur l’ion $Cr^{3+}$

‐action de l’ion dichromate $Cr_{2}O_{7}^{2‐}$sur l’ion $Fe^{2+}$

‐action de l’ion permanganate $MnO_{4}^{‐}$ sur l’ion $Fe^{2+}$

$$\begin{array}{|c|c|c|c|c|}
\hline
\text{Couple}&    S_{2}O_{8}^{2‐} /SO_{4}^{2‐}    &MnO_{4}^{‐} /Mn^{2+}    &Cl_{2}/Cl‐ &    Cr_{2}O_{7}^{2‐}/ Cr^{3+}&    Fe^{3+}/Fe^{2+} \\
\hline
\text{Potentiel d’oxydoréduction} E^{0} (V)&    2,10&    1,51&    1,39&    1,33    &0,77\\
\hline
\end{array}$$

2. Dosage en retour : sur une prise d’essai d’acier $35 CD 4$ de masse $m = 1 g$, on réalise les opérations indiquées.

Dans la solution à doser contenant l’ion dichromate, on verse un excès, soit $V_{1} = 15mL$ d’une solution de sel de $Mohr$ de concentration molaire volumique $c_{1}= 0,1mol.L^{‐1}$

La solution de sel de $Mohr$ a été acidifiée par de l’acide sulfurique.  

L’excès de sel de $Mohr$ est dosé par une solution de permanganate de potassium de concentration molaire volumique $c_{2} = 0,02 mol.L^{‐1}$

Il faut verser $V_{2}= 9,3cm^{3}$ de cette solution pour obtenir une teinte rose persistante.

Déterminer la teneur en chrome, exprimée en $%$ massique, de l’acier étudié.

Conclusion.
 
On donne la Masse molaire atomique du Chrome $Cr = 52g.mol^{‐1}$

EXERCICE 16    Elimination des ions cuivre

Une entreprise spécialisée dans la récupération des métaux précieux désire éliminer d'une eau polluée les ions $Cu^{2+}$ qu'elle contient.

Pour cela, on immerge dans cette eau des barres d'acier que l'on assimile à du fer pur.

1. Écrire l'équation représentant les couples $Fe^{2+}/Fe$ et $Cu^{2+}/Cu$.

2. En comparant les valeurs de leurs potentiels standards, expliquer quelle est la réaction spontanée se produisant entre ces deux couples.

Écrire les équations représentant:

-l'oxydation

-la réduction

-la réaction globale d'oxydo

-réduction.

3. Expliquer comment le procédé utilisé dans cet atelier permet d'éliminer les ions $Cu^{2+}$ de l'eau.

4. On traite $500L$ d'eau polluée. Quand la réaction est terminée, on récupère 317,5g de cuivre.
Déterminer la concentration en ions Cu2+ de l'eau polluée en $mol.L^{-1}$

5. Les ions $Fe^{2+}$ apparus au cours du traitement de cette eau sont éliminés à l'aide d'une solution d'hydroxyde de sodium.

Un précipité d'hydroxyde de $fer II [Fe(OH)2]$ se forme.

5.1. Écrire l'équation de la réaction entre les ions $Fe^{2+}$ et les ions $OH^{-}$

5.2. Quel volume d'une solution d'hydroxyde de sodium de concentration $c=2,5mol.L^{-1}$ doit-on alors verser dans les $500L$ d'eau traitée?

Données : $E^{0} (Cu^{2+} /Cu)= 0,34V$  et $E^{0} (Fe^{2+}/ Fe)=-0,44V$

EXERCICE 17

Le zinc des gouttières s’abime sous l’action des pluies acides.

En plongeant une lame de zinc dans une solution aqueuse d’acide, on constate une disparition progressive du métal et un dégagement gazeux (qui explose à la moindre étincelle).

1. Action des pluies acides sur le zinc

Les deux couples oxydant/réducteur mis en jeu sont : $H^{+}/H_{2}$ de potentiel redox $E^{0} = 0,00V$ et $Zn^{2+}/Zn$ de potentiel redox $E^{0} = - 0,76V$

1.1. L’association de ces deux couples constitue une pile.

1.1.1. Quelle serait la borne moins de cette pile ?
1.1.2. Donner la valeur de la force électromotrice E attendue pour cette pile.

1.2. A quelle borne de la pile y a-t-il oxydation ?

1.3. Donner l'équation globale de la réaction de fonctionnement de cette pile.

2. Action des pluies acides sur le cuivre

Les deux couples oxydants/réducteurs mis en jeu sont : $H^{+}/H_{2}$ de potentiel redox $E^{0} = 0,00V$ et $Cu^{2+}/Cu$ de potentiel redox $E^{0}= + 0,34V$.

2. l. L’association de ces deux couples constitue une pile.

Quelle est la valeur de la force électromotrice E attendue pour cette pile.

2.2. A quelle borne de la pile y a-t-il réduction ?

2.3. Donner l’équation globale de la réaction de fonctionnement de cette pile.

3. Conclusion

3. l. Quel est le gaz dégagé qui explose dans l’air à la moindre étincelle lorsque l’on plonge le zinc dans une solution acide ?

3.2. Expliquer pourquoi, indépendamment du coût, la gouttière en cuivre sera préférée à la gouttière en zinc dans les régions ou les pluies acides sont fréquentes.

EXERCICE 18

On constitue une pile à l’aide d’une électrode constituée du couple $(Ag^{+}/Ag)$ et d’une électrode constituée par le couple $(Cr_{2}O_{7}^{2}-/Cr^{3+})$.

Ce dernier couple est obtenu en utilisant une solution de dichromate de potassium, une solution de sulfate de chrome $(III)$ et une solution d’acide sulfurique.

Les conditions de l’expérience sont les conditions standards.

1. Donner la formule chimique de la solution de dichromate de potassium ainsi que sa concentration.

2. Donner la formule chimique de la solution de sulfate de chrome $(III)$ ainsi que sa concentration.

3. Donner la formule chimique de la solution d’acide sulfurique ainsi que sa concentration.

4. Comment réaliser l’électrode $(Ag^{+}/Ag)$ ?

Donner la concentration de la solution utilisée.

5. Faire le schéma de la pile ainsi constituée. Préciser les polarités en les justifiant.

Indiquer le sens du courant traversant le circuit et le circuit du mouvement des électrons.

6. Calculer la force électromotrice de la pile en début de fonctionnement.
Données : $E° (Ag+/Ag)= 0,80V ; E°(Cr_{2}O_{7}^{2-}/Cr^{3+})= 1,33V$

EXERCICE 20   Corrosion et protection

On cherche à protéger une canalisation en fonte (alliage
contenant essentiellement du fer) enfouie dans le sol.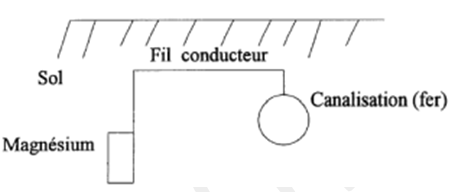

1. Citer au moins un oxydant (molécule, ion) susceptible, dans ces conditions d'enfouissement, d'oxyder le fer en ion $Fe^{2+}$

La suite de l'exercice est consacrée à la protection de cette canalisation     

Celle-ci est reliée à une électrode de magnésium à l'aide d'un fil conducteur (voir schéma ci-dessus).

On admet que le pouvoir réducteur du couple $Mg^{2+}/Mg$ est supérieur à celui du couple $Fe^{2+}/Fe$.

2. Expliquer pourquoi le magnésium est capable de protéger la canalisation.

3. Écrire les demi-équations électrochimiques qui se produisent sur la canalisation en fonte et sur l'électrode de magnésium.

Indiquer l'oxydation et la réduction. Donner l'équation globale d'oxydoréduction.

4. Donner le sens de circulation des électrons dans ce montage. Indiquer l'anode et la cathode.

5. Citer deux autres méthodes de protection des métaux contre la corrosion

EXERCICE 21    Qualité dans les industries alimentaires et les bio-industries

La composition chimique du vin est d'une grande complexité : plusieurs centaines de corps y participent.

Ils proviennent directement du raisin ou sont produits au cours de la fermentation alcoolique et des transformations bactériennes.

On y trouve de l'eau, de l'éthanol, des acides organiques (acide tartrique, acide citrique ...), du dioxyde de soufre (surtout dans les vins blancs), des sucres, des substances minérales (fer, cuivre à l'état d'ions)...

Dosage de l'éthanol d'un vin

- On place, dans un ballon rôdé, $20,0mL$ de vin, $200mL$ d'eau distillée, on distille ce mélange.

On obtient $50,0 mL$ de distillat qu'on verse dans une fiole jaugée de $250 mL$.

On complète avec de l'eau distillée, cette solution est notée $S_{1}$.

- On prélève $10,0 mL$ de $S_{1}$ auxquels on ajoute $V_{2} = 20,0 mL$ de solution de dichromate de potassium
($K_{2}Cr_{2}O_{7}$) de concentration $C_{2} = 0,115mol·L^{–1}$ et $10 mL$ d'acide sulfurique concentré.

- On dose l'excès d'ions dichromate par les ions fer II d'une solution de sel de $Mohr$.

La concentration des ions $Fe^{2+}$ est $C_{1} = 0,700mol·L^{–1}$.

Le volume équivalent est $V_{1} = 10,3mL$.

1. Écrire l'équation de la réaction d'oxydation de l'éthanol en acide éthanoïque par les ions dichromate.

2. Écrire l'équation de la réaction entre les ions de dichromate en excès et les ions fer $II$.

3.1. Calculer la quantité de matière d'ions dichromate en excès.

3.2. Calculer la quantité de matière d'ions dichromate ayant réagi avec l'éthanol.

3.3. Calculer la quantité de matière d'éthanol présente dans $10,0mL$ de solution $S_{1}$.

4. Calculer la quantité de matière puis la concentration en éthanol contenu dans l'échantillon de vin initial.

5. La teneur en alcool d'un vin est exprimée par son pourcentage en volume : volume d'éthanol liquide
(En litres à $20° C$) dissout dans un volume total de $100L$ de mélange.

Déterminer le pourcentage volumique en éthanol du vin étudié (encore appelé degré alcoolique).   Données :

- potentiels standards (à $25° C)  Cr_{2}O_{7}^{2–}/ Cr^{3+} : 1,33V ; Fe^{3+}/ Fe^{2+} : 0,77 V
CH_{3}–COOH / CH_{3}–CH_{2}OH : 0,035V$

- Masse volumique de l'éthanol à $20° C : 789g·L^{–1}$.

- Masses molaires en $g·mol^{–1} : M(H) = 1 ; M(C) = 12 ; M(O) = 16$

EXERCICE 22  Le dioxyde de soufre un polluant atmosphérique

Le dioxyde de soufre $(SO_{2})$, provenant de la combustion des combustibles fossiles (charbons, gaz naturels, dérivés du pétrole comme le fioul lourd par exemple) et des rejets de l'industrie chimique, est un des polluants atmosphériques responsables des pluies acides.

Mais le dioxyde de soufre est également un intermédiaire chimique industriel important utilisé par exemple dans la synthèse de l'acide sulfurique $(H_{2}SO_{4})$.

Pour lutter contre cette pollution on peut agir de manière préventive en diminuant la teneur en soufre des produits pétroliers mais aussi de manière curative en traitant les effluents (fumées et rejets industriels) avant leur libération à l'atmosphère

Contrôle chimique de la teneur en $SO_{2}$ (gaz) dans un effluent gazeux d'une cheminée.

Le dioxyde de soufre étant très soluble dans l'eau on fait barboter lentement un volume de $0,1 m^{3}$ d'air, prélevé à proximité de la sortie de la cheminée, dans $50 mL$ d'eau distillée de façon à obtenir $50 mL$ d'une solution aqueuse incolore de dioxyde de soufre.

On réalise un dosage d'oxydoréduction de cette préparation par une solution acidifiée de permanganate de potassium $(K^{+}, MnO_{4–})$ de couleur violette et de concentration molaire volumique $C_{1} = 2,5·10^{–3} mol· L^{–1}$.

Le volume de la solution de permanganate de potassium nécessaire pour obtenir l'équivalence est
$V_{éq} = 12mL$.

On rappelle que pour le couple $MnO_{4} –/ Mn^{2+}$ la demi-équation électronique correspondante s'écrit :
 $MnO_{4} –+ 8 H^{+} + 5e^{–}      Mn^{2+} + 4H_{2}O $

1. Écrire pour l'autre couple intervenant (voir les données) la demi-équation électronique correspondante.

2. Écrire l'équation globale d'oxydoréduction intervenant au cours de ce dosage en justifiant son sens.

3. Expliquer le changement de couleur qui permet de repérer l'équivalence.
 
Quel est le nombre de moles d'ions permanganate contenus dans les $12mL$ utilisés pour obtenir l'équivalence ?

4. En déduire le nombre de moles de dioxyde de soufre dans les $50 mL$ de solution préparée puis vérifier que l'effluent gazeux analysé contient $7, 5.10^{–4}$ mole de $SO_{2}$ par $m^{3}$.

5. Sachant que les normes de la $CEE$ fixent une teneur massique en $SO_{2}$ de $250µg·m^{–3}$, comparer cette valeur à la teneur massique en $SO_{2}$ de l'effluent. Conclure.
 
Données :

- Potentiels standard $E°$ en $V : SO_{4}^{2–} / SO_{2} : 0,17 ;  MnO_{4–}/ Mn^{2+} : 1,51$ (violet)/ (incolore)

- Masses molaires atomiques en $g·mol^{–1} : S = 32 ; O = 16 $

EXERCICE 23

On plonge une lame de cuivre dans une solution de sulfate ferreux (cas 1) et une autre dans une solution de nitrate d’argent (cas 2).

1. Donner les formules des solutions de sulfate ferreux et de nitrate d’argent.

2. Qu’observe-t-on dans chaque cas ?

Expliquer.

3. Calculer le potentiel d’une demi-pile composée d’une lame de platine plongeant dans une solution contenant $1,0.10^{-1} mol.L^{-1}$ d’ions ferreux et $1,0.10^{-3} mol.L^{-1}$ d’ions ferriques.

4. Calculer le potentiel d’une demi-pile composée d’une lame de cuivre plongeant dans une solution contenant 1$0^{-1} mol.L^{-1}$ d’ions cuivriques.

5. On associe ces deux demi-piles.

5.1. Faire un schéma de la pile en indiquant les polarités des électrodes, le sens de circulation des électrons dans le circuit extérieur.

5.2. Quelle est la $f.é.m$. de cette pile ?

5.3. Ecrire l’équation de la réaction de fonctionnement.

Données : $E°(Fe^{2+} /Fe) = -0,44V ; E°(Ag+/Ag) = 0,80 V ; E°(Fe^{3+} / Fe^{2+} ) = 0,77 V ; E°(Cu^{2+} /Cu)= 0,34 V$

EXERCICE 24

On dose un volume $V_{Red} = 10 mL$ d'une solution $(S)$ de sel de $Mohr$ de formule $Fe(SO_{4})2(NH_{4})2,6H_{2}O$ par une solution acidifiée de permanganate de potassium $KMnO_{4}$ de concentration molaire $COx = 0,012 mol.L^{-1}$.

L'équivalence est obtenue pour un volume $VOx.E$ égal à $12,5 mL$ de la solution titrante.

1. Ecrire l'équation chimique de la réaction de dosage sachant qu'elle met en jeu les deux couples redox $Fe^{3+}/Fe^{2+}$ et $MnO_{4-}/Mn^{2+}$.

2. Calculer la concentration $C_{Red}$ de la solution $(S)$.

3. Calculer la masse m de sel de $Mohr$ nécessaire pour préparer $1L$ de la solution $(S) $

EXERCICE 25

Le sulfate de fer $(II)$ hydraté se présente sous la forme de cristaux verts de formule $FeSO_{4}, nH_{2}O$.

On se propose de déterminer $n$.

Pour cela, on prépare une solution $(S)$ de ce sel de concentration massique
$C = 30,0 g.L^{-1}$.

1. Décrire le mode de préparation de $100 mL$ de $(S)$.

2. Comment caractériser la présence d'ions fer $(II)$ dans $(S)$ ?

3. On dose un volume $V_{Red} =10,0 mL$ de la solution $(S)$ par une solution acidifiée de permanganate de potassium de concentration molaire $COx = 0,020 mol.L^{-1}$.

3.1. Décrire le dispositif expérimental nécessaire pour réaliser ce dosage en précisant la verrerie utilisée.

3.2. Comment peut-on repérer l'équivalence ?

3.3. Le volume versé à l'équivalence est $VOx.E =10,8 mL$.

Déterminer la concentration molaire de la solution $(S)$.

3.4.  En déduire la valeur du nombre $n$.

EXERCICE 26

Dans un laboratoire de lycée, on se propose de préparer $250 mL$ d’une solution de permanganate de potassium $KMnO_{4}$, de concentration $CO = 2. 10^{-2} mol/L$.

A partir des cristaux de permanganate de potassium.

1. Quelle masse de cristaux faut-il peser ?

2. Donner en quelques lignes, le mode opératoire nécessaire à la préparation de cette solution en précisant la verrerie utilisée.

3. On utilise la solution de permanganate de potassium précédente pour doser une solution de dioxyde de soufre en milieu acide.

3.1. A quoi sert le dosage ?

3.2. Comment reconnait-on l’équivalence dans ce dosage ?

3.3. Faire un schéma annoté du dispositif expérimental du dosage.

3.4. Ecrire l’équation bilan de la réaction de dosage, sachant que les potentiels standards des
couples mis en jeu sont $E° (MnO^{4−}/Mn^{2+}) = 1,51 v$ et $E°(SO8{4}^{2−}/SO_{2}) = 0,17 v$.

3.5. Montrer que cette réaction est totale.

3.6. Déterminer la concentration molaire de la solution de dioxyde de soufre dont on a utilisé $10ml$ pour ce dosage, sachant que l’équivalence est atteinte lorsqu’on a versé $8,6 mL$ de permanganate de potassium.
 
Données : masses molaires atomiques $(en g/mol) : K = 39,1 ; Mn = 54,9 ; O = 16$

EXERCICE 27

Au laboratoire, lorsque l’on ne dispose pas d’une bouteille de dioxygène comprimé, on peut préparer ce gaz en faisant réagir en milieu acide une solution de permanganate de potassium sur de l’eau oxygénée $H_{2} O_{2}$ à $20$ volumes.

Cette indication, portée sur

l’étiquette signifie que, dans les conditions normales de pression et de température, elle peut libérer un volume de dioxygène égal à $20$ fois le volume d’eau oxygénée utilisé : $1L$ de solution libère $20 L$ de dioxygène.

Dans cette réaction, l’eau oxygénée appartient au couple :$ H_{2}O_{2} / H_{2}O$

1. Ecrire l’équation de la réaction d’oxydoréduction.

2. Quel volume d’eau oxygénée faut-il utiliser pour obtenir 1L de dioxygène ?

3. La solution de permanganate de potassium a une concentration $c=0,25 mol/L$.

Quel volume minimal de cette solution doit-on introduire dans le flacon ?

EXERCICE 28   Éthylotest

Peu après avoir été consommé, l’alcool (éthanol de formule $CH_{3}CH_{2}OH$) passe dans le sang au niveau de l’intestin grêle.

Ensuite, des échanges gazeux s’effectuent dans les alvéoles pulmonaires :

le sang se charge en dioxygène et se libère du dioxyde de carbone ainsi que d’une partie de l’alcool.

Ces vapeurs sont expirées dans l’air avec une concentration en alcool $2100$ fois inférieure à celle du sang.

Le seuil limite autorisé pour la conduite est de $0,50 g$ d’éthanol par litre de sang.

Les alcootests jetables sont constitués d’un sachet gonflable de capacité 1L et d’un tube en verre contenant des cristaux orangés de dichromate de potassium $K_{2}Cr_{2}O_{7}$ en milieu acide.

Ceux-ci se colorent en vert au contact de l’alcool.

Données :

- Potentiels standard : couple $Cr_{2}OO_{7}^(2-)/Cr^{3+} E_{1^{◦}} = 1,33V$ ; couple $CH_{3}COOH/CH_{3}CH_{2}OH E_{2^{◦}} = 0,19 V $;

-Masses molaires atomiques : $M_{H} = 1g·mol^{−1} ; M_{C} = 12 g· mol^{−1} ; MO = 16 g ·mol^{−1} ; M_{K} = 39 g·mol^{−1 ;
M_{Cr} = 52 g· mol^{−1}$.

1. Écrire l’équation de la transformation responsable du changement de couleur.
 
Identifier l’espèce oxydée et l’espèce réduite.

2. Calculer la constante d’équilibre de la réaction. Commenter.

3. Déterminer la quantité de matière d’alcool expirée par litre d’air dans l’hypothèse d’une alcoolémie atteignant le seuil de $0,50 g$ d’alcool par litre de sang.

4. En déduire la masse de dichromate de potassium devant être placée avant le trait de jauge afin que celui-ci indique le seuil limite.

EXERCICE 29 Dosage colorimétrique en retour

On s’intéresse à un dosage colorimétrique d’une solution de dichromate de potassium par les ions fer $(II)$ dans en milieu sulfurique garantissant un $pH$ très acide.

On donne les potentiels standard $E◦_{1} = E◦(Cr_{2}O_{7}^{2-}/Cr^{3+}) = 1,33V$ et $E_{2}◦ = E◦(Fe^{3}+/Fe^{2+}) = 0,77 V $.

En milieu acide, l’ion dichromate est orange et l’ion chrome $(III)$ est vert, alors que l’ion $Fe^{2+}$ est vert pâle et l’ion Fe3+ est jaune-orangé.

1. Écrire l’équation bilan du titrage redox direct.

2. On effectue un dosage en retour.

Dans un bécher, on verse $V_{1} = 4,0 mL$ de la solution de dichromate de potassium dont on cherche la concentration $C_{1}$.

On y ajoute $V_{2} = 10,0 mL$ d’une solution de sulfate de fer $(II)$ en milieu sulfurique de concentration  $C_{2} = 0,10 mol·L^{-1}$ et $90,0 mL$ d’eau.

On verse ensuite par une burette une solution de permanganate de potassium de concentration
$C_{3} = 1,0·10^{-2} mol·L^{-1}$.

Une coloration violette, caractéristique du permanganate en solution, apparaît lorsque $V_{3E} = 12mL$ ont été versés.

4. Comment peut-on s’assurer qualitativement que les ions fer $(II)$ ont bien été apportés en excès par rapport au dichromate ?

5. Écrire l’équation bilan du titrage en retour.

6. Déterminer la concentration$ C_{1}$ de la solution de dichromate de potassium